PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BT
11 tháng 5 2017
a)Do \(0^o< \alpha< 90^o\) nên \(0< sin\alpha< 1;0< cos\alpha< 1\).
Giả sử: \(tan\alpha< sin\alpha\Leftrightarrow\dfrac{sin\alpha}{cos\alpha}< sin\alpha\)
\(\Leftrightarrow sin\alpha< sin\alpha cos\alpha\)
\(\Leftrightarrow sin\alpha\left(1-cos\alpha\right)< 0\)
\(\Leftrightarrow1-cos\alpha< 0\)
\(\Leftrightarrow cos\alpha>1\) (vô lý).
b) \(sin\alpha+cos\alpha=sin\alpha+sin\left(\dfrac{\pi}{2}-\alpha\right)\)
\(=2.sin\dfrac{\pi}{4}cos\left(\dfrac{\pi}{4}-\alpha\right)=\sqrt{2}cos\left(\dfrac{\pi}{4}-\alpha\right)\)
\(=\sqrt{2}sin\left(\dfrac{\pi}{4}+\alpha\right)=\sqrt{2}sin\left(45^o+\alpha\right)\).
Do \(0^o< \alpha< 90^o\) nên \(45^o< \alpha+45^o< 135^o\).
Vì vậy \(\dfrac{\sqrt{2}}{2}< sin\left(\alpha+45^o\right)< 1\).
Từ đó suy ra \(\sqrt{2}.sin\left(45^o+\alpha\right)>\sqrt{2}.\dfrac{\sqrt{2}}{2}=1\) (Đpcm).
CM
18 tháng 3 2017
Chọn A.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay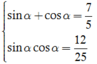 
vào P ta được 
CM
22 tháng 4 2018
Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do 
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy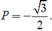 
13 tháng 4 2016
Từ M kẻ MP ⊥ Ox, MQ ⊥ Oy
=> = cosα;
=
= sinα;
Trong tam giác vuông MPO:
MP2+ PO2 = OM2 => cos2 α + sin2 α = 1
TK
0
T
2
7 tháng 2 2019
Dùng bất đẳng thức phụ:(x+y)2≥4xy
Ta có (a+b)2≥4ab ;(c+b)2≥4cb;(a+c)2≥4ac
⇒(a+b)2(b+c)2(a+c)2≥64(abc)2
do đó (a+b)(b+c)(c+a)≥8abc
Dấu “=” xảy ra khi a = b = c
7 tháng 2 2019
AD BĐT cô si cho số không âm
(a+b)(a+c)(b+c)\(\ge\)\(2\sqrt{ab}.2\sqrt{ac}.2\sqrt{bc}\)=8\(\sqrt{\left(abc\right)^2}\)=8abc
AH
Akai Haruma
Giáo viên
11 tháng 3 2019
Lời giải:
Vì \(x,y,z\in [0;1]\Rightarrow xy; yz,xz\geq xyz\)
\(\Rightarrow P=\frac{x}{1+yz}+\frac{y}{1+xz}+\frac{z}{xy+1}\leq \frac{x}{1+xyz}+\frac{y}{1+xyz}+\frac{z}{1+xyz}=\frac{x+y+z}{xyz+1}(*)\)
\(x,y,z\in [0;1]\Rightarrow \left\{\begin{matrix} (x-1)(y-1)\geq 0\\ (xy-1)(z-1)\geq 0\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} xy+1\geq x+y\\ xyz+1\geq xy+z\end{matrix}\right.\)
\(\Rightarrow xyz+2+xy\geq x+y+z+xy\)
\(\Leftrightarrow xyz+2\geq x+y+z\)
Mà: \(xyz+2\leq 2xyz+2=2(xyz+1)\)
\(\Rightarrow x+y+z\leq 2(xyz+1)(**)\)
Từ \((*); (**)\Rightarrow P\leq \frac{2(xyz+1)}{xyz+1}=2\) (đpcm)
Dấu "=" xảy ra khi \((x,y,z)=(1,1,0)\)
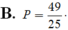
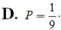
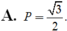
Ta có sinα + cosα > 0 và sinαcosα > 0. Do đó
( sin α + cos α ) 2 = sin 2 α + cos 2 α + 2 sin α cos α
= 1 + 2sinαcosα > 1
Từ đó suy ra: sinα + cosα > 1