Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có giá trị trung bình:
\(\overline x = \frac{0,398 + 0,399 + 0,408 + 0,410 + 0,406 + 0,405 + 0,402}{7}\)
\( = 0,404\)
Ta có bảng sau:
Giá trị | Độ lệch | Bình phương độ lệch |
0,398 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,399 | 0,005 | \(2,{5.10^{ - 5}}\) |
0,408 | 0,004 | \(1,{6.10^{ - 5}}\) |
0,410 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,406 | 0,002 | \(0,{4.10^{ - 5}}\) |
0,405 | 0,001 | \(0,{1.10^{ - 5}}\) |
0,402 | 0,002 | \(0,{4.10^{ - 5}}\) |
Tổng | \(12,{2.10^{ - 5}}\) |
Phương sai:
\({s^2} = \frac{{12,{{2.10}^{ - 5}}}}{7} \approx 0,000017\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 4,{17.10^{ - 3}}\)
Phép đo có độ chính xác cao.

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{ABC}+59^0+82^0=180^0\)
=>\(\widehat{ABC}=39^0\)
Xét ΔABC có \(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
=>\(\dfrac{25}{sin39}=\dfrac{AB}{sin82}\)
=>\(AB=25\cdot\dfrac{sin82}{sin39}\simeq39,34\left(m\right)\)

Bình phương hai vế ta được:
\(\begin{array}{l}{(8 - 40x)^2} + {(7 - 40x)^2} = 25\\ \Leftrightarrow 64 - 640x + 1600{x^2} + 49 - 560x + 1600{x^2} = 25\\ \Leftrightarrow 3200{x^2} - 1200x + 88 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{11}}{{40}}\\x = \frac{1}{{10}}\end{array} \right.\end{array}\)
Vậy phương trình có hai nghiệm là \(x = \frac{{11}}{{40}}\) và \(x = \frac{1}{{10}}\).

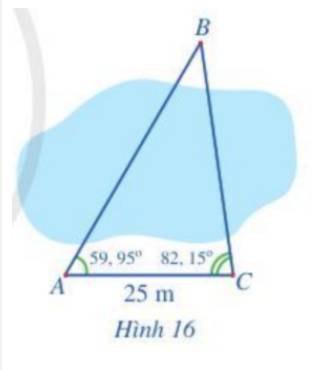
Xét tam giác ABC, ta có: \(\widehat {BAC} = 59,{95^o};\;\widehat {BCA} = 82,{15^o}.\)
\( \Rightarrow \widehat {ABC} = {180^o} - \left( {59,95 + 82,{{15}^o}} \right) = 37,{9^o}\)
Áp dụng định lí sin trong tam giác BAC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AB = \sin C.\frac{{AC}}{{\sin B}} = \sin 82,{15^o}.\frac{{25}}{{\sin {37,9^o}}} \approx 40\)
Vậy khoảng cách từ vị trí A đến vị trí B là 40 m.

a) Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là
\(R = {x_{\max }} - {x_{\min }} = 16 - 14 = 2\)
b) +) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:
2 5 6 7 8 9 10 11 12 14 16
+) Vậy \({Q_1}{\rm{ }} = 6;{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}9;{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}12\) . Suy ra \({Q_3} - {Q_1}{\rm{ = }}12{\rm{ }} - 6 = 6\)

a) Nhà máy A:
+) Số trung bình: \(\overline x = \frac{{4 + 5 + 5 + 47 + 5 + 6 + 4 + 4}}{8} = 10\)
+) Mốt: \({M_o} = 4,{M_o} = 5\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 4; 4; 4; 5; 5; 5; 6; 47.
\({Q_2} = {M_e} = 5\)
\({Q_1}\) là trung vị của nửa số liệu: 4; 4; 4; 5. Do đó \({Q_1} = 4\)
\({Q_3}\) là trung vị của nửa số liệu: 5; 5; 6; 47. Do đó \({Q_3} = 5,5\)
+) Phương sai \({S^2} = \frac{1}{8}\left( {{4^2} + {5^2} + ... + {4^2}} \right) - {10^2} = 196\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 14\)
Nhà máy B:
+) Số trung bình: \(\overline x = \frac{{2 + 9 + 9 + 8 + 10 + 9 + 9 + 11 + 9}}{9} = 8,4\)
+) Mốt: \({M_o} = 9\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 8; 9; 9; 9; 9; 9; 10; 11
\({Q_2} = {M_e} = 9\)
\({Q_1}\) là trung vị của nửa số liệu: 2; 8; 9; 9. Do đó \({Q_1} = 8,5\)
\({Q_3}\) là trung vị của nửa số liệu: 9; 9; 10; 11. Do đó \({Q_3} = 9,5\)
+) Phương sai \({S^2} = \frac{1}{9}\left( {{2^2} + {9^2} + ... + {9^2}} \right) - 8,{4^2} = 6,55\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 2,56\)
b)
Nhà máy A có: \({\Delta _Q} = 1,5\)
Vậy giá trị ngoại lệ \(x > 5,5 + 1,5.1,5 = 7,75\) hoặc \(x < 4 - 1,5.1,5 = 1,75\) là 47.
Nhà máy B có: \({\Delta _Q} = 1\)
Vậy giá trị ngoại lệ \(x > 9,5 + 1,5.1 = 11\) hoặc \(x < 8,5 - 1,5.1 = 7\) là 2.
Ta so sánh trung vị: \(9 > 5\), do dó công nhân nhà máy B có mức lương cao hơn.
Chú ý
Ta không so sánh số trung bình vì có giá trị 47 quá lớn so với các giá trị còn lại.

Giải tam giác là việc đi tìm một số yếu tố của tam giác khi đã biết các yếu tố khác của tam giác đó.
Trong trường hợp này, giải tam giác ABC được hiểu là tìm cạnh AC khi biết cạnh AB, góc A và góc B.
Áp dụng định lí sin ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
Mà \(AB=d, \hat {B} =\beta; \hat {C} =180^o-\alpha -\beta \)
\(\Rightarrow AC = \sin \beta \frac{d}{{\sin \left( {{{180}^o} - \alpha - \beta } \right)}}\)

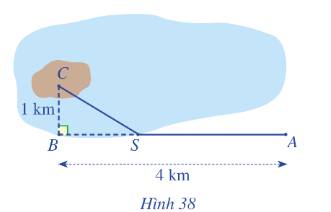
Gọi khoảng cách từ A đến S là x (km) (0<x<4)
\( \Rightarrow BS = 4 - x\)(km)
\( \Rightarrow CS = \sqrt {C{B^2} + B{S^2}} \)\( = \sqrt {1 + \left( {4 - {x^2}} \right)} \)(km)
Tổng số tiền từ A đến C là:
\(3.SA + 5.SC = 3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} \)(triệu đồng)
Khi đó ta có phương trình:
\(3.x + 5.\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16\)
\( \Leftrightarrow 5\sqrt {1 + {{\left( {4 - x} \right)}^2}} = 16 - 3x\)
\(\begin{array}{l}25.\left( {{x^2} - 8x + 17} \right) = {\left( {16 - 3x} \right)^2}\\ \Leftrightarrow 25{x^2} - 200x + 425 = 256 - 96x + 9{x^2}\\ \Leftrightarrow 16{x^2} - 104x + 169 = 0\\ \Leftrightarrow x = \frac{{13}}{4}\left( {tm} \right)\end{array}\)
Do \(16 - 3x > 0 \Leftrightarrow \forall 0 < x < 4\)
=> \(SC = \sqrt {1 + \left( {4 - {x^2}} \right)} = 1,25\)
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)

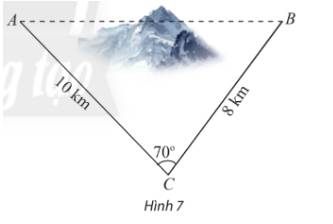
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}A{B^2} = B{C^2} + A{C^2} - 2.BC.AC.\cos C\\ \Leftrightarrow A{B^2} = {8^2} + {10^2} - 2.8.10.\cos {70^o}\\ \Rightarrow AB \approx 10,45\end{array}\)
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
\(AC + CB - AB = 10 + 8 - 10,45 = 7,55\;(km).\)
Sắp xếp các giá trị theo thứ tự không giảm:
0,2900,290 0,3980,398 0,3990,399 0,4010,401 0,4020,402 0,4020,402 0,4050,405 0,4060,406 0,4080,408 0,4100,410
Tứ phân vị thứ nhất là 399399, tứ phân vị thứ ba là 406406, do đó \Delta_Q=7ΔQ=7.
Đoạn số liệu không bất thường là [Q_1-1,5 \Delta_QQ1−1,5 ΔQ ; Q_3+1,5 \Delta_QQ3+1,5ΔQ] = [388,5388,5 ; 416,5416,5].
Theo đoạn số liệu không bất thường, ta thấy 0,2090,209 không thuộc đoạn này, do đó kết luận của Bình là hợp lí.