Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)

Một hình cầu có số đo diện tích (đơn vị: m2) bằng số đo thể tích (đơn vị: m3). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.
Hướng dẫn làm bài:
Gọi R là bán kính hình cầu (đơn vị : mét)
Khi đó ta có: S = 4πR2 và V=4/3 πR3
Theo đề bài ta có: 4πR2=4/3πR3⇒R/3=1⇒R=3(m)
Ta có: S = 4πR2 = 4π . 32 = 36π (m2)
V=4/3 π R3=4/3 π.33=36π(m3)

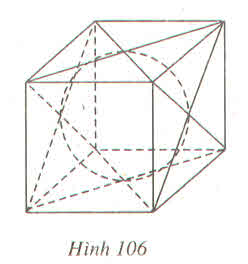
Ta thấy ngay cạnh của hình lập phương gấp đôi bán kính hình cầu
a) Tỉ số cần tính \(\dfrac{6}{\pi}\)
b) Diện tích toàn phần của hình lập phương là \(42cm^2\)
c) Thể tích cần tính xấp xỉ \(244cm^3\)

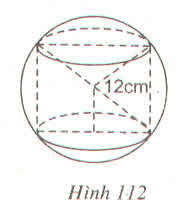
a) Diện tích xung quanh của hình trụ : \(288\pi\left(cm^2\right)\)
b) Thể tích hình cầu : \(2304\pi\left(cm^3\right)\)
c) Diện tích mặt cầu : \(576\pi\left(cm^2\right)\)

a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3



a, Tính được S = 64π c m 2 và V = 256 π 3 c m 3
b, Tính được S = 211,32π c m 2