
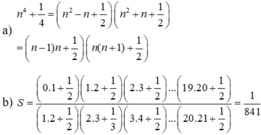
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

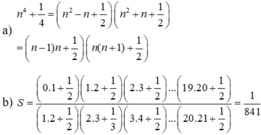

Ta có:
\(1^4+\frac{1}{4}=\left(1^2-1+\frac{1}{2}\right)\left(1^2+1+\frac{1}{2}\right)=\frac{1}{2}.\left(2+\frac{1}{2}\right)\)
\(2^4+\frac{1}{4}=\left(2^2-2+\frac{1}{2}\right)\left(2^2+2+\frac{1}{2}\right)=\left(2+\frac{1}{2}\right).\left(6+\frac{1}{2}\right)\)
\(3^4+\frac{1}{4}=\left(3^2-3+\frac{1}{2}\right)\left(3^2+3+\frac{1}{2}\right)=\left(6+\frac{1}{2}\right).\left(12+\frac{1}{2}\right)\)
\(4^4+\frac{1}{4}=\left(4^2-4+\frac{1}{2}\right)\left(4^2+4+\frac{1}{2}\right)=\left(12+\frac{1}{2}\right).\left(20+\frac{1}{2}\right)\)
...
\(19^4+\frac{1}{4}=\left(19^2-19+\frac{1}{2}\right)\left(19^2+19+\frac{1}{2}\right)=\left(342+\frac{1}{2}\right).\left(380+\frac{1}{2}\right)\)
\(20^4+\frac{1}{4}=\left(20^2-20+\frac{1}{2}\right)\left(20^2+20+\frac{1}{2}\right)=\left(380+\frac{1}{2}\right).\left(420+\frac{1}{2}\right)\)
=> \(\frac{\left(1^4+\frac{1}{4}\right)\left(3^4+\frac{1}{4}\right)\left(5^4+\frac{1}{4}\right)...\left(19^4+\frac{1}{4}\right)}{\left(2^4+\frac{1}{4}\right)\left(4^4+\frac{1}{4}\right)\left(6^4+\frac{1}{4}\right)...\left(20^4+\frac{1}{4}\right)}\)
\(=\frac{\frac{1}{2}\left(2+\frac{1}{2}\right)\left(6+\frac{1}{2}\right)\left(12+\frac{1}{2}\right)...\left(342+\frac{1}{2}\right).\left(380+\frac{1}{2}\right)}{\left(2+\frac{1}{2}\right)\left(6+\frac{1}{2}\right)\left(12+\frac{1}{2}\right)\left(20+\frac{1}{2}\right)...\left(380+\frac{1}{2}\right).\left(420+\frac{1}{2}\right)}\)
\(=\frac{\frac{1}{2}}{420+\frac{1}{2}}=\frac{1}{841}\)

a) \(x^4-2x^3+2x-1\)
\(=x^4-x^3-x^3+2x-2+1\)
\(=\left(x^4-x^3\right)+\left(2x-2\right)-\left(x^3-1\right)\)
\(=x^3\left(x-1\right)+2\left(x-1\right)-\left(x-1\right)\left(x^2+x+1\right)\)
\(=\left(x-1\right)\left(x^3+2-x^2-x-1\right)\)
\(=\left(x-1\right)\left(x^3-x^2-x+1\right)\)
\(=\left(x-1\right)\left[\left(x^3-x^2\right)-\left(x-1\right)\right]\)
\(=\left(x-1\right)\left[x^2\left(x-1\right)-\left(x-1\right)\right]\)
\(=\left(x-1\right)\left(x^2-1\right)\left(x-1\right)\)
\(=\left(x-1\right)^2\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)^3\left(x+1\right)\)
b) \(x^4+2x^3+2x^2+2x+1\)
\(=\left(x^4+2x^2+1\right)+\left(2x^3+2x\right)\)
\(=\left(x^2+1\right)^2+2x\left(x^2+1\right)\)
\(=\left(x^2+1\right)\left(x^2+1+2x\right)\)
\(=\left(x^2+1\right)\left(x+1\right)^2\)

a) \(\left(x+1\right)^4-\left(x-1\right)^4=\left[\left(x+1\right)^2\right]^2-\left[\left(x-1\right)^2\right]^2\)
\(=\left[\left(x+1\right)^2-\left(x-1\right)^2\right].\left[\left(x+1\right)^2+\left(x-1\right)^2\right]\)
\(=\left(x+1-x+1\right)\left(x+1+x-1\right)\left(x^2+2x+1+x^2-2x+1\right)\)
\(=2.2x.\left(2x^2+2\right)=8x\left(x^2+1\right)\)
b) \(\left(x^2-25\right)^2-4\left(x+5\right)^2=\left[\left(x-5\right)\left(x+5\right)\right]^2-4\left(x+5\right)^2\)
\(=\left(x+5\right)^2\left[\left(x-5\right)^2-4\right]=\left(x+5\right)^2\left(x^2-10x+25-4\right)=\left(x+5\right)^2\left(x^2-10+21\right)\)
\(=\left(x+5\right)^2\left(x-3\right)\left(x-7\right)\)

1) x4y2 + x2y4 + x4y3 + x2y5 = (x4y2 + x2y4) + (x4y3 + x2y5) = x2y2.(x2 + y2) + x2y3.(x2 + y2) = x2y2.(x2+ y2) (1 + y) = [xy.(x2 + y2)].[xy(1+y)]
=> x4y2 + x2y4 + x4y3 + x2y5 chia cho xy.(x2 + y2) bằng xy.(1+ y)
2) A = (n2 - 8)2 + 36 = n4 - 16n2 + 100 = (n4 + 20n2 + 100) - 36n2 = (n2 + 10)2 - (6n)2 = (n2 - 6n+ 10).(n2 + 6n+ 10)
Vậy để A là số nguyên tố thì n2 - 6n + 10 = 1 hoặc n2 + 6n + 10 = 1
Mà n là số tự nhiên nên n2+ 6n + 10 > 1
=> n2 - 6n + 10 = 1 => n2 - 6n + 9 = 0 => (n -3)2 = 0 => n = 3
Vậy....
3) a) = xy(x - y) - xz(x + z) + yz.[(x+ z) + (x - y)] = xy(x - y) - xz(x + z) + yz.(x + z) + yz(x - y)
= [xy(x - y) + yz.(x - y)] + [(yz.(x+ z) - xz(x+z)] = y(x - y)(x+ z) + z(x + z).(y - x) = (x+ z)(x- y).(y - z)
b) = (x2 + x)2 - (2x)2 - 4(x+3) = (x2 + x + 2x).(x2 + x- 2x) - 4(x+3) = (x2 + 3x).(x2 - x) - 4(x+3)
= (x+3).[x.(x2 - x) - 4] = (x+3).(x3 - x2 - 4) = (x+3).(x3 - 8 + 4 - x2) = (x+3).[(x - 2)(x2 + 2x + 4) - (x - 2).(x+2)]
= (x + 3).(x - 2).(x2 + 2x + 4 - x- 2) = (x + 3).(x - 2).(x2 + x + 2)
4) a) n4 + 1/4 = (n4 + n2 + 1/4) - n2 = (n2 + 1/2)2 - n2 = (n2 - n + 1/2).(n2 + n + 1/2) = [n(n - 1) + 1/2].[n.(n+1) + 1/2]
Áp dụng công thức ta có:
A = \(\frac{\left(1^4+\frac{1}{4}\right)\left(3^4+\frac{1}{4}\right)...\left(19^4+\frac{1}{4}\right)}{\left(2^4+\frac{1}{4}\right).\left(4^4+\frac{1}{4}\right)...\left(20^4+\frac{1}{4}\right)}=\frac{\frac{1}{2}.\left(1.2+\frac{1}{2}\right).\left(2.3+\frac{1}{2}\right).\left(3.4+\frac{1}{2}\right)...\left(18.19+\frac{1}{2}\right).\left(19.20+\frac{1}{2}\right)}{\left(1.2+\frac{1}{2}\right).\left(2.3+\frac{1}{2}\right).\left(3.4+\frac{1}{2}\right).\left(4.5+\frac{1}{2}\right)...\left(19.20+\frac{1}{2}\right).\left(20.21+\frac{1}{2}\right)}\)
A = \(\frac{\frac{1}{2}}{20.21+\frac{1}{2}}=\frac{1}{841}\)