Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề 1:Phần I:Trắc nghiệm.
Câu 1:Cho đoạn thẳng BC = 4cm, gọi I là trung điểm của BC. Hỏi đoạn thẳng BI dài bao nhiêu cm ?
| A.1 | B.2 | C.3 | D.4 |
Câu 2:Cho a,b ⛇ N, b ≠ 0, a ⋮ b thì:
| A. a là ước của b | B. a là bội của b |
Câu 3:Cho tập hợp E = {1;2;a;b}{1;2;a;b}. Cách viết nào sau đây là đúng ?
| A. {1;2}{1;2} ⛇ E | B. 0 ⛇ E | C. {1;2}{1;2} ⊂ E | D. 2 ⊂ E |
Câu 4:Trên đường thẳng xy, lấy 3 điểm A, B, C phân biệt. Số đoạn thẳng được tạo thành là:
| A. 1 | B. 4 | C. 2 | D. 3 |
Câu 5:Số đối của ||-8||+2 là:
| A. -10 | B. -8 | C. 8 | D. -6 |
Câu 6: Qua 3 điểm phân biệt không thẳng hàng số đường thẳng vẽ được là:
| A. 6 | B. 1 | C. 3 | D. 2 |
Câu 7:Với a = 4; b = 5 thì tích a22.b bằng bao nhiêu ?
| A. 30 | B. 100 | C. 80 | D. 40 |
Câu 8;Cho -6 < x ≤ 5. Tổng các số nguyên x bằng:
| A. 0 | B. -1 | C. -6 | D. -5 |
Câu 9:BCNN(10,14,16) là:
| A. 5.7 | B. 244 | C. 2.5.7 | D. 244.5.7 |
Câu 10: Cho hình vẽ sau, khẳng định nào là đúng:
| A. a cắt b | B. a trùng b | C. a song song b | D. a bằng b |
Câu 11:Cho tập hợp Y = {x⊓N|x≤9}{x⊓N|x≤9}. Số phần tử của Y là:
| A. 7 | B. 10 | C. 9 | D.8 |
Câu 12:Điểm M là trung điểm của đoạn thẳng AB khi :
| A. AM + MB = AB |
| B. MA = MB |
| C. AM + MB = AB và MA = MB |
| D. M nằm giữa A và B |
Câu 13:Trong các tập hợp sau đây, tập hợp nào chỉ gồm các số nguyên tố:
| A. {2;5;7;9;11;13}{2;5;7;9;11;13} |
| B. {1;2;35;7;11}{1;2;35;7;11} |
| C. {2;3;5;7;11;13}{2;3;5;7;11;13} |
| D. {3;5;7;13;15;17}{3;5;7;13;15;17} |
Câu 14:Tổng của các số nguyên x thỏa mãn -3 < x ≤ 2 là:
| A. 5 | B. 0 | C. -3 | D. 6 |
Câu 15:Cho tập hợp P = {x∈N⋅|x≤4}{x∈N⋅|x≤4}. Khi viết tập hợp P bằng cách liệt kê các phần tử, thì:
| A. P = {1;2;3}{1;2;3} |
| B. P = {1;2;3;4}{1;2;3;4} |
| C. P = {0;1;2;3}{0;1;2;3} |
| D. P = {0;1;2;3;4}{0;1;2;3;4} |
Câu 16:Khẳng định nào sau đây là đúng;
| A. Nếu một số chia hết cho 3 thì số đó cũng chia hết cho 9 |
| B. Nếu a là phần tử của tập hợp A thì ta viết a ⊂ A |
| C. Nếu (a+b) ⋮ m thì a ⋮ m và b ⋮ m |
| D. Cả A, B, C đều sai |
Câu 17:Diểm I là trung điểm của đoạn thẳng AB khi:
| A. I nằm giữa A và B |
| B. IA = IB |
| C. IA =IB và IA + IB = AB |
| D. IB = AB2AB2 |
Câu 18:Cho các số nguyên -15; 30; -1; 0; -279. Thứ tự sắp xếp các số nguyên theo thứ tự giảm dần là;
| A. -279; -15; -1; 0; 30 |
| B. -1; -15; -279; 0; 30 |
| C. 30; 0; -1; -15; -279 |
| D. -279; 30; -15; -1; 0 |
Câu 19:Cho 4 điểm M, N, P, Q cùng nằm trên đường thẳng sao cho điểm M nằm giữa N và P, điểm Q nằm giữa M và N. Chỉ ra đáp án sai:
| A. Điểm M nằm giữa N và Q |
| B. Hai điểm M và Q nằm cùng phía đối với điểm P |
| C. Điểm M nằm giữa N và P |
| D. ĐIểm M nằm giữa P và Q |
Câu 20:Cho ƯCLN(a,b) = 2, BCNN(a,b) = 12. Khi đó a,b bằng:
| A.6 | B.12 | C.24 | D.2 |
Câu 21:Cho 4 điểm A, B, C, D thẳng hàng. Có số đoạn thẳng là:
| A.4 | B.6 | C.5 | D. Một kết quả khác |
Câu 22:Trên đường thẳng d lấy 3 điểm A, B, C sao cho A nằm giữa B và C. Chỉ ra đáp án sai:
| A. Tia CBvà tia CA trùng nhau |
| B. Tia AB và tia CA trùng nhau |
| C. Ba điểm A, B, C thẳng hàng |
| D. Tia AB và tia AC đối nhau |
Đề j mà dài dữ zậy !!! ( mỏi tay )
![]()
![]()
![]()
![]()
![]()

| a | \(\dfrac{-2}{3}\) | \(\dfrac{4}{15}\) | \(\dfrac{9}{4}\) | \(\dfrac{5}{9}\) | \(\dfrac{5}{4}\) | \(\dfrac{4}{16}\) | 0 | \(\dfrac{12}{18}\) | \(\dfrac{-4}{10}\) | 0 |
| b | \(\dfrac{4}{5}\) | \(\dfrac{5}{8}\) | \(\dfrac{-2}{3}\) | \(\dfrac{5}{14}\) | \(\dfrac{-2}{4}\) | 1 | \(\dfrac{-5}{12}\) | 0 | \(\dfrac{-17}{42}\) | |
| a.b | \(\dfrac{-8}{5}\) | \(\dfrac{1}{6}\) | \(\dfrac{-3}{2}\) | \(\dfrac{25}{126}\) | \(\dfrac{-5}{8}\) | \(\dfrac{4}{16}\) | 0 | \(\dfrac{12}{18}\) | 0 | 0 |

| NHÂN | \(\frac{2}{3}\) | \(\frac{-5}{6}\) | \(\frac{7}{12}\) | \(\frac{-1}{24}\) |
| \(\frac{2}{3}\) | \(\frac{4}{9}\) | \(\frac{-5}{9}\) | \(\frac{7}{18}\) | \(\frac{-1}{36}\) |
| \(\frac{-5}{6}\) | \(\frac{-5}{9}\) | \(\frac{25}{36}\) | \(\frac{-35}{72}\) | \(\frac{5}{144}\) |
| \(\frac{7}{12}\) | \(\frac{7}{18}\) | \(\frac{-35}{72}\) | \(\frac{49}{144}\) | \(\frac{-7}{288}\) |
| \(\frac{-1}{24}\) | \(\frac{-1}{36}\) | \(\frac{5}{144}\) | \(\frac{-7}{288}\) | \(\frac{1}{576}\) |
nhân | 2/3 | -56 | 7/12 | -1/24 |
| 2/3 | 4/9 | -5/9 | 7/18 | -1/36 |
| -5/6 | -5/9 | 25/36 | -35/72 | 5/144 |
| 7/12 | 7/18 | -35/72 | 49/144 | -7/288 |
| -1/24 | -1/5 | 5/144 | -7/288 | 1/576 |

a=-3/4; b=4/7 =>ab=-3/7
\(a=\dfrac{5}{9};b=-\dfrac{18}{15}=-\dfrac{6}{5}\Leftrightarrow ab=-\dfrac{2}{3}\)
\(a=-\dfrac{7}{25};b=\dfrac{50}{21}\Leftrightarrow ab=-\dfrac{2}{3}\)
\(ab=1;b=-\dfrac{3}{7}\Leftrightarrow a=-\dfrac{7}{3}\)
\(a=\dfrac{4}{7};b=-\dfrac{3}{4}\Leftrightarrow ab=-\dfrac{3}{7}\)
\(a=\dfrac{-4}{19};ab=-\dfrac{4}{19}\Leftrightarrow b=1\)
\(a=-\dfrac{18}{15}=-\dfrac{6}{5};c=\dfrac{5}{9}\Leftrightarrow ab=-\dfrac{2}{3}\)
\(ab=0;b=\dfrac{6}{13}\Leftrightarrow a=0\)

Câu 3 :
a) Đặt n2 + 2006 = a2 (a\(\in\)Z)
=> 2006 = a2 - n2 = (a - n)(a + n) (1)
Mà (a + n) - (a - n) = 2n chia hết cho 2
=>a + n và a - n có cùng tính chẵn lẻ
+)TH1: a + n và a - n cùng lẻ => (a - n)(a + n) lẻ, trái với (1)
+)TH2: a + n và a - n cùng chẵn => (a - n)(a + n) chia hết cho 4, trái với (1)
Vậy không có n thỏa mãn n2+2006 là số chính phương
b)Vì n là số nguyên tố lớn hơn 3 => n không chia hết cho 3
=> n = 3k + 1 hoặc n = 3k + 2 (k \(\in\)N*)
+) n = 3k + 1 thì n2 + 2006 = (3k + 1)2 + 2006 = 9k2 + 6k + 2007 chia hết cho 3 và lớn hơn 3
=> n2 + 2006 là hợp số
+) n = 3k + 2 thì n2 + 2006 = (3k + 2)2 + 2006 = 9k2 + 12k + 2010 chia hết cho 3 và lớn hơn 3
=> n2 + 2006 là hợp số
Vậy n2 + 2006 là hợp số
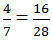 chữ B ứng với số 16
chữ B ứng với số 16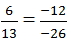 chữ I ứng với số -12
chữ I ứng với số -12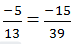 chữ N ứng với số -15
chữ N ứng với số -15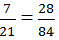 chữ T ứng với số 84
chữ T ứng với số 84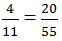 chữ U ứng với số 55
chữ U ứng với số 55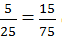 chữ O ứng với số 75
chữ O ứng với số 75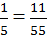 chữ H ứng với số 11
chữ H ứng với số 11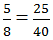 chữ A ứng với số 25
chữ A ứng với số 25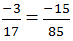 chữ G ứng với số 85
chữ G ứng với số 85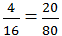 chữ D ứng với số 80
chữ D ứng với số 80