Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm

\(A=0.5\cdot4\sqrt{3-x}-\sqrt{3-x}-2\sqrt{3}+1=\sqrt{3-x}-2\sqrt{3}+1\) (xác định khi x=<3)
a)thay \(x=2\sqrt{2}\)vào a ra có
\(\sqrt{3-2\sqrt{2}}-2\sqrt{3}+1=\sqrt{\left(\sqrt{2}-1\right)^2}-2\sqrt{3}+1\)
\(=\sqrt{2}-1+2\sqrt{3}+1=\sqrt{2}+2\sqrt{3}\)
Để A=1<=> \(\sqrt{3-x}-2\sqrt{3}+1=1\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}+1-1=0\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}=0\\ \Leftrightarrow3-x=12\Leftrightarrow x=-9\)

đề : Cho đoạn thẳng AB cùng điểm C thuộc đoạn thẳng đó (C khác A và B). Về cùng một nửa mặt phẳng bờ AB, kẻ hai tia Ax và By cùng vuông góc với AB. Trên tia Ax lấy điểm M cố định. Kẻ tia Cz vuông góc với tia CM tại C, tia Cz cắt tia By tại K. Vẽ đường tròn tâm O đường kính MC cắt MK tại E

bài 41
:
Gọi x là số mà một bạn (Minh hoặc Lan) đã chọn và số mà bạn kia chọn là x + 5.
Khi đó tích của hai số là x(x+5).
Theo đề bài ta có phương trình x(x+ 5) = 150
Vậy:
Nếu bạn Minh chọn số 10 thì bạn Lan chọn số 15 hoặc ngược lại.
Nếu bạn Minh chọn số -15 thì bạn Lan chọn số -10 hoặc ngược lại.
bài 42:
Gọi lãi suất cho vay là x (%), x > 0
Tiền lãi sau một năm là: 2 000 000 . x/100 hay 20000x (đồng)
Sau 1 năm cả vốn lẫn lãi sẽ là: 2 000 000 + 20000x (đồng)
Tiền lãi riêng năm thứ hai phải chịu là:
(2 000 000 + 20000x) x/100
hay 20000x + 200x2
Số tiền sau hai năm bác Thời phải trả là:
2 000 000 + 40000x + 200x2
Theo đầu bài ra ta có phương trình:
2 000 000 + 40 000x + 200x2 = 2 420 000 hay x2 + 200x – 2 100 = 0
Giải phương trình:
∆’ = 1002 – 1 . (-2 100) = 10 000 + 2 100 = 12 100
=> √∆’ = 110
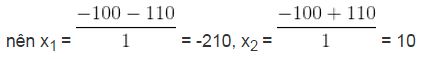
Vì x > 0 nên x1 không thỏa mãn điều kiện của ẩn.
Trả lời: lãi suất là 10%.
bài 43;
Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vận tốc lúc về là x – 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là:
120/x + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
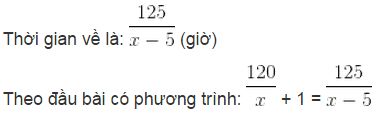
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h.
.
còn bài nào gửi lên mình trả lời cho.
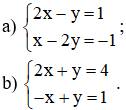



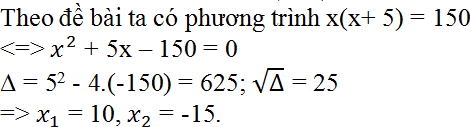
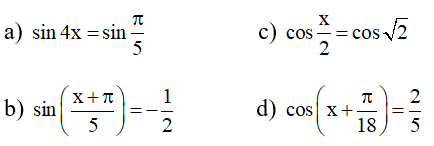
Mình cần gấp huhu
a: \(\left\{{}\begin{matrix}2x-y=1\\x-2y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x-1\\2y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x-1\\y=\dfrac{1}{2}x+1\end{matrix}\right.\)
Vì \(2< >\dfrac{1}{2}\)
nên hai đường thẳng y=2x-1 và y=1/2x+1 sẽ cắt nhau tại 1 điểm duy nhất
=>Hệ sẽ có 1 nghiệm
b: \(\left\{{}\begin{matrix}2x+y=4\\-x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-2x+4\\y=x+1\end{matrix}\right.\)
Vì -2<>1 nên hai đường thẳng y=-2x+4 và y=x+1 sẽ cắt nhau tại 1 điểm duy nhất
=>Hệ sẽ có 1 nghiệm duy nhất