
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
\(\Rightarrow2\left(5x-2\right)=3\left(5-3x\right)\)
\(\Leftrightarrow10x-4=15-9x\)
\(\Leftrightarrow10x+9x=15+4\)
=> 19x = 19
=> x = 1
Ta có :
\(\Leftrightarrow\frac{10x+3}{12}=\frac{9}{9}+\frac{6+8x}{9}\)
\(\Leftrightarrow\frac{10x+3}{12}=\frac{15+8x}{9}\)
=> (10x + 3)9 = (15 + 8x).12
=> 90x + 27 = 180 + 96x
=> 90x - 96x = 180 - 27
=> -6x = 153
=> -x = 25,5
=> x = -25,5

\(\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{6}{2x}+\dfrac{6}{y}=\dfrac{1}{4}\)
\(\Leftrightarrow6\left(\dfrac{1}{2x}+\dfrac{1}{y}\right)=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{2x}+\dfrac{1}{y}=\dfrac{1}{24}^{\left(1\right)}\)
Lại có: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}^{\left(2\right)}\)
Lấy (2) trừ (1) ta có:
\(\dfrac{1}{x}+\dfrac{1}{y}-\dfrac{1}{2x}-\dfrac{1}{y}=\dfrac{1}{16}-\dfrac{1}{24}\)
\(\Leftrightarrow\dfrac{2-1}{2x}=\dfrac{1}{48}\)
\(\Leftrightarrow\dfrac{1}{2x}=\dfrac{1}{48}\)
=> 2x = 48
<=> x = 24
Thay x = 24 vào (2) ta có:
\(\dfrac{1}{24}+\dfrac{1}{y}=\dfrac{1}{16}\)
\(\Leftrightarrow\dfrac{1}{y}=\dfrac{1}{48}\)
=> y = 48
Vậy ...
Ta có: \(\dfrac{3}{x}\) + \(\dfrac{6}{y}\) = \(\dfrac{1}{4}\)
<=> 3(\(\dfrac{1}{x}\) + \(\dfrac{2}{y}\) ) = \(\dfrac{1}{4}\)
<=> \(\dfrac{1}{x}\) + \(\dfrac{2}{y}\) = \(\dfrac{1}{12}\) (1)
Mặt khác: \(\dfrac{1}{x}\) + \(\dfrac{1}{y}\) = \(\dfrac{1}{16}\) (2)
Trừ (2) cho (1) vế theo vế ta được:
\(\dfrac{1}{x}\) + \(\dfrac{2}{y}\) - \(\dfrac{1}{x}\) - \(\dfrac{1}{y}\) = \(\dfrac{1}{12}\) - \(\dfrac{1}{16}\)
<=> \(\dfrac{1}{y}\) = \(\dfrac{1}{48}\) <=> y = 48
Thay y =48 vào (2) ta có: \(\dfrac{1}{x}\) + \(\dfrac{1}{48}\) = \(\dfrac{1}{16}\)
<=> \(\dfrac{1}{x}\) = \(\dfrac{1}{24}\) <=> x = 24
Vậy x =24 ; y =48

Ta có :
\(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+....+\frac{1}{\left(x+5\right)\left(x+6\right)}\)
\(=\frac{1}{x}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+2}+....+\frac{1}{x+5}-\frac{1}{x+6}\)
\(=\frac{1}{x}-\frac{1}{x+6}\)
\(=\frac{6}{x\left(x+6\right)}\)

a) Góc ngoài còn lại: 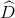 =3600 – (750 + 900 + 1200) = 750
=3600 – (750 + 900 + 1200) = 750
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là:
1050, 900, 600, 1050
b)Hình 7b SGK:
Tổng các góc trong  +
+  +
+ +
+ =3600
=3600
Nên tổng các góc ngoài
 +
+  +
+ +
+ =(1800 -
=(1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  )
)
=(1800.4 - ( 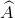 +
+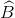 +
+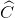 +
+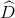 )
)
=7200 – 3600 =3600
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng 3600
học tốt

Bài 1:
a: \(5x^3-x^2-5x+1\)
\(=x^2\left(5x-1\right)-\left(5x-1\right)\)
\(=\left(5x-1\right)\left(x-1\right)\left(x+1\right)\)
b: \(x^2+4xy+4y^2-9\)
\(=\left(x+2y\right)^2-9\)
\(=\left(x+2y+3\right)\left(x+2y-3\right)\)
c: \(x^2-5x+6=\left(x-2\right)\left(x-3\right)\)

b)\(\frac{3xy+3}{9y+3}\)=\(\frac{3\left(xy+1\right)}{3\left(3y+1\right)}\)=\(\frac{xy+1}{3y+1}\) khác \(\frac{x}{3}\) sửa lại \(\frac{3xy+3}{9y+3}\)=\(\frac{xy+1}{3y+1}\)
c)\(\frac{3xy+3}{9y+3}\)=\(\frac{3\left(xy+1\right)}{3\left(3y+1\right)}\)=\(\frac{xy+1}{3y+1}\) khác \(\frac{x+1}{3+3}\) và \(\frac{x+1}{3+3}\)
\(\frac{x+1}{3+3}\)=\(\frac{x+1}{6}\)