Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

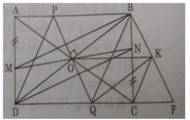
c) PQ ⊥ BD (gt). Xét các tam giác vuông POB và QOD có:
∠POB = ∠QOD∠ (đối đỉnh),
OB = OD
∠PBO = ∠QDO (so le trong).
Do đó ΔPOB = ΔQOD (g.c.g) ⇒ BP = DQ
Lại có BP // DQ nên tứ giác PBQD là hình bình hành
Mặt khác PBQD có hai đường chéo vuông góc nên là hình thoi.

1: AM+MB=AB
BN+NC=BC
CP+PD=CD
QD+QA=AD
mà AB=BC=CD=AD và AM=BN=CP=QD
nên BM=CN=PD=QA
2: Xét ΔMAQ vuông tại A và ΔNBM vuông tại B có
MA=NB
AQ=BM
Do đó: ΔMAQ=ΔNBM
=>MQ=MN(1)
Xét ΔMBN vuông tại B và ΔNCP vuông tại C có
MB=NC
BN=CP
Do đó: ΔMBN=ΔNCP
=>MN=NP(2)
Xét ΔNCP vuông tại C và ΔPDQ vuông tại D có
NC=PD
CP=DQ
Do đó: ΔNCP=ΔPDQ
=>NP=PQ(3)
Từ (1),(2),(3) suy ra MQ=MN=NP=PQ
ΔMAQ=ΔNBM
=>\(\widehat{AMQ}=\widehat{BNM}\)
mà \(\widehat{BNM}+\widehat{BMN}=90^0\)(ΔBMN vuông tại B)
nên \(\widehat{AMQ}+\widehat{BMN}=90^0\)
\(\widehat{AMQ}+\widehat{QMN}+\widehat{NMB}=180^0\)
=>\(90^0+\widehat{QMN}=180^0\)
=>\(\widehat{QMN}=90^0\)
Xét tứ giác MNPQ có
MN=NP=PQ=MQ
nên MNPQ là hình thoi
Hình thoi MNPQ có \(\widehat{QMN}=90^0\)
nên MNPQ là hình vuông