Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác CAOM có
góc CAO+góc CMO=180 độ
nên CAOM là tứ giác nội tiếp
b: Xét (O) có
CA,CM là tiêp tuyến
nên CA=CM và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
CM*MD=OM^2
=>CA*BD=R^2
c: CA=CM
OA=OM
=>CO là trung trực của AM
=>CO vuông góc với AM
=>CO//BK
Xét ΔABK có
O là trung điểm của AB
OC//BK
Do đó: C là trung điểm của AK

c.
\(CM=AC\) (t/c 2 tiếp tuyến cắt nhau) (1)
\(\widehat{KMC}=\widehat{DMB}\) (đối đỉnh)
Mà \(DM=DB\) (t/c 2 tiếp tuyến cắt nhau) \(\Rightarrow\Delta DMB\) cân tại D
\(\Rightarrow\widehat{DMB}=\widehat{DBM}\Rightarrow\widehat{KMC}=\widehat{DBM}\)
Lại có: \(\widehat{DBM}=\widehat{AKB}\) (cùng phụ \(\widehat{ABK}\))
\(\Rightarrow\widehat{KMC}=\widehat{AKB}\Rightarrow\Delta CKM\) cân tại C
\(\Rightarrow CK=CM\) (2)
(1);(2) \(\Rightarrow CK=CA\) hay C là trung điểm AK
d.
Qua A kẻ đường thẳng song song BM cắt BD kéo dài tại E
\(\Rightarrow AKBE\) là hbh (2 cặp cạnh đối song song)
\(\Rightarrow\) 2 đường chéo KE và AB cắt nhau tại trung điểm O của AB
Hay K, O, E thẳng hàng
Theo t/c 2 tiếp tuyến ta có \(OD\perp BM\) \(\Rightarrow OD\perp AE\)
Đồng thời \(AB\perp DE\) (gt)
\(\Rightarrow\) O là trực tâm tam giác ADE
\(\Rightarrow OE\perp AD\)
\(\Rightarrow OK\perp AD\)

a: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
CD=CM+MD
=>CD=CA+BD
c: AC*BD=MC*MD=OM^2=R^2 ko đổi
d: CM=CA
OM=OA
Do đó: CO là trung trực của AM
mà H nằm trên đường trung trực của AM
nên O,H,C thẳng hàng

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN//AC//BD
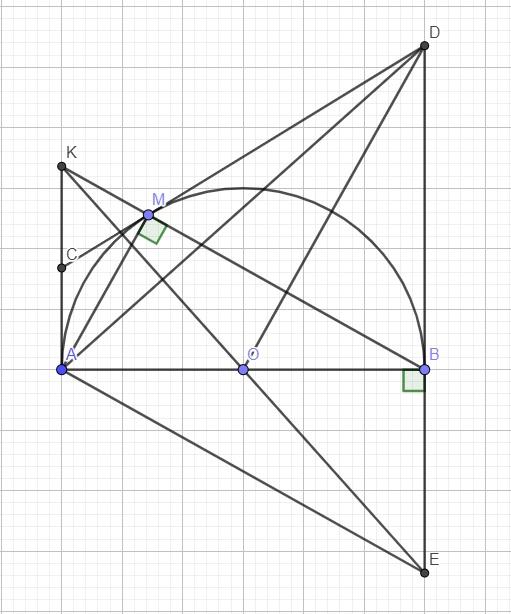
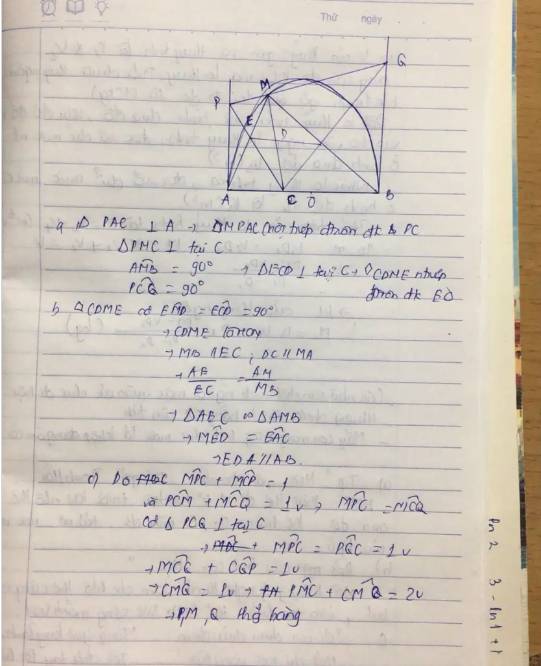
a: Xét tứ giác CAOK co
góc CAO+góc CKO=180 độ
nên CAOK là tứ giác nội tiếp
b: Xét (O) có
CK,CA là tiếp tuyến
nên CK=CA và OC là phân giác của góc AOK(1)
Xét (O) có
DK,DB là tiếp tuyến
nên DK=DB và OD là phân giác của góc KOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
OK^2=KC*KD
=>AC*BD=R^2 ko đổi
c: Xét ΔOAK có OA=OK=AK
nên ΔOAK đều
=>gócc AOK=60 độ
=>góc KOB=120 độ
=>góc KDB=60 độ
mà DK=DB
nên ΔDKB đều