K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HG
9
5 tháng 10 2021
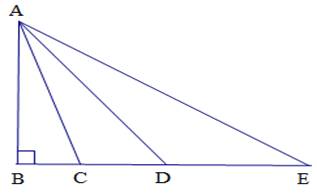
Điểm C nằm giữa B và D nên BC < BD (1)
Điểm C nằm giữa B và E nên BD < BE (2)
Vì B, C, D, E thẳng hàng. Từ (1) và (2) suy ra
BC < BD < BE
AB⊥BE
Suy ra: AB < AC < AD < AE.
LM
5 tháng 10 2021
+ Ta có BC < BD < BE.
Mà AC, AD, AE là các đường xiên tương ứng với các hình chiếu BC, BD, BE
Suy ra AC < AD < AE.
+ AB là đường vuông góc nên AB nhỏ nhất trong tất cả các đường xiên và đường vuông góc.
Do đó AB < AC < AD < AE.
^HT^
HG
4
16 tháng 9 2021
a) \(=\frac{25}{36}\)
b) \(=\frac{50}{7}\)
c) \(=\frac{200}{279}\)
16 tháng 9 2021
a) 1,2: 3,24 = 120 : 324 = 10:27
b) 215:34215:34 = 115:34=115.43=44:15115:34=115.43=44:15
c) 27:0,4227:0,42 = 27:42100=27.10042=200294=100147=100:14727:42100=27.10042=200294=100147=100:147
LD
1
TL
0
Giải:
Ta có: Xét tam giác vuông ABC vuông tại B nên cạnh AC là cạnh huyền, ta có:
AC > AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
\(\widehat{ADB}\) < 900 (vì tam giác ADB vuông tại B)
\(\widehat{ACD}\) = \(\widehat{ABC}\) + \(\widehat{BAC}\) (Góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
⇒ \(\widehat{ACD}\) = 900 + \(\widehat{BAC}\) > \(\widehat{ADB}\) = \(\widehat{ADC}\)
Xét tam giác ADC có:
\(\widehat{ACD}\) > \(\widehat{ADC}\) (cmt)
AD > AC (2)(Trong tam giác góc đối diện với cạnh lớn hơn thì lớn hơn và ngược lại)
Chứng minh tương tự ta có:
AE > AD (3)
Từ (1) và (2) và (3) ta có:
AE > AD > AC > AB
Kết luận: AE > AD > AC > AB