
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)

4:
a: -90<a<0
=>cos a>0
cos^2a=1-(-4/5)^2=9/25
=>cosa=3/5
\(sin\left(45-a\right)=sin45\cdot cosa-cos45\cdot sina=\dfrac{\sqrt{2}}{2}\left(cosa-sina\right)\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{3}{5}-\dfrac{4}{5}\right)=\dfrac{-\sqrt{2}}{10}\)
b: pi/2<a<pi
=>cosa<0
cos^2a+sin^2a=0
=>cos^2a=16/25
=>cosa=-4/5
tan a=3/5:(-4/5)=-3/4
\(tan\left(a+\dfrac{pi}{3}\right)=\dfrac{tana+\dfrac{tanpi}{3}}{1-tana\cdot tan\left(\dfrac{pi}{3}\right)}\)
\(=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\dfrac{-3}{4}\cdot\sqrt{3}}=\dfrac{48-25\sqrt{3}}{11}\)
c: 3/2pi<a<pi
=>cosa>0
cos^2a+sin^2a=1
=>cos^2a=25/169
=>cosa=5/13
cos(pi/3-a)
\(=cos\left(\dfrac{pi}{3}\right)\cdot cosa+sin\left(\dfrac{pi}{3}\right)\cdot sina\)
\(=\dfrac{5}{13}\cdot\dfrac{1}{2}+\dfrac{-12}{13}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{5-12\sqrt{3}}{26}\)

5:
a: sin x=2*cosx
\(A=\dfrac{6cosx+2cosx-4\cdot8\cdot cos^3x}{cos^3x-2cosx}\)
\(=\dfrac{8-32cos^2x}{cos^2x-2}\)
b: VT=sin^4(pi/2-x)+cos^4(x+pi/2)+6*1/2*sin^22x+1/2*cos4x
=cos^4x+sin^4x+3*sin^2(2x)+1/2*(1-2*sin^2(2x))
=1-2*sin^2x*cos^2x+3*sin^2(2x)+1/2-sin^2(2x)
==3/2=VP


a) Bảng phân bố tần số (về tuổi thọ bóng đèn điện) có thể viết dưới dạng như sau:

Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:
.(3x1150 + 6x1160 + 12x1170 + 6x1180 + 3x1190)
= 1170.
b) Số trung bình về chiều dài lá cây dương xỉ trong bài tập 2 trong là:
.(8x15 + 18x25 + 24x35 + 10x45) = 31 (cm).

a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
![]()
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.

23.
Gọi I là trung điểm MN \(\Rightarrow I\left(3;3\right)\)
\(\Rightarrow\overrightarrow{IN}=\left(2;-1\right)\Rightarrow IN=\sqrt{5}\)
Phương trình đường tròn đường kính MN, nhận I là tâm và có bán kính \(R=IN\) là:
\(\left(x-3\right)^2+\left(y-3\right)^2=5\)
Thay tọa độ E vào pt ta được:
\(\left(x-3\right)^2+4=5\Rightarrow\left(x-3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\) \(\Rightarrow x_1x_2=8\)
Cả 4 đáp án của câu này đều sai
24.
Gọi \(M\left(x;y\right)\) là 1 điểm bất kì thuộc \(\Delta\)
Do \(\Delta\) là đường phân giác của góc tạo bởi d và k nên:
\(d\left(M;d\right)=d\left(M;k\right)\Leftrightarrow\dfrac{\left|2x+y\right|}{\sqrt{2^2+1^2}}=\dfrac{\left|x+2y-3\right|}{\sqrt{1^2+2^2}}\)
\(\Leftrightarrow\left|2x+y\right|=\left|x+2y-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+y=x+2y-3\\2x+y=-x-2y+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-y+3=0\\x+y-1=0\end{matrix}\right.\)
- Với \(x-y+3=0\), ta có:
\(\left(x_E-y_E+3\right)\left(x_F-y_F+3\right)=2.1=2>0\Rightarrow E;F\) nằm cùng phía so với \(x-y+3=0\) (thỏa mãn)
- Với \(x+y-1=0\) ta có:
\(\left(x_E+y_E-1\right)\left(x_F+y_F-1\right)=2.7=14>0\Rightarrow E;F\) nằm cùng phía so với \(x+y-1=0\) (thỏa mãn)
Vậy cả đáp án A và D đều đúng
Tương tự như câu 23, câu 24 đề bài tiếp tục sai

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.
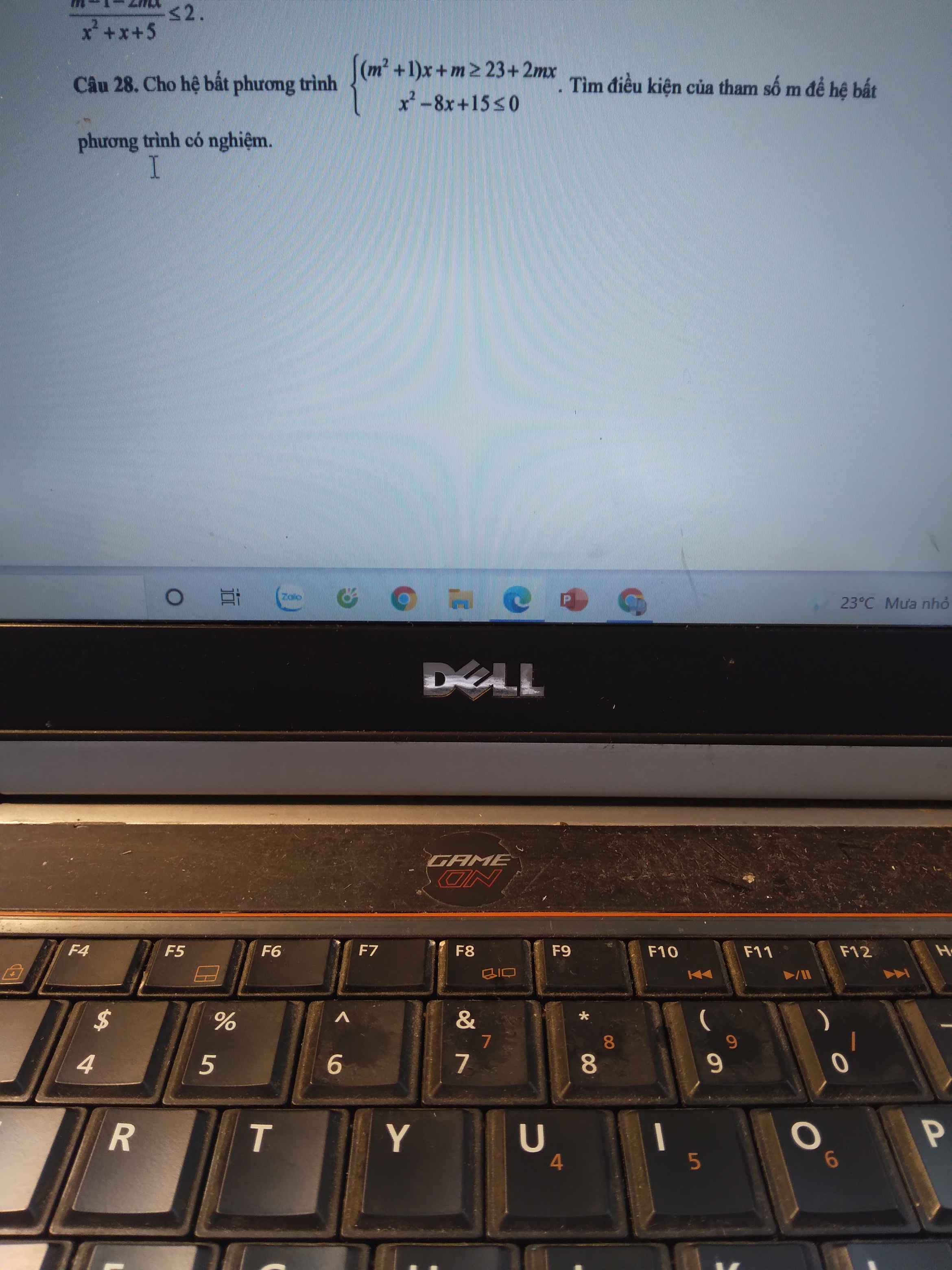













Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)
Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)
\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)
\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)
- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)
- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)
\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)
Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)
\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)
\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)