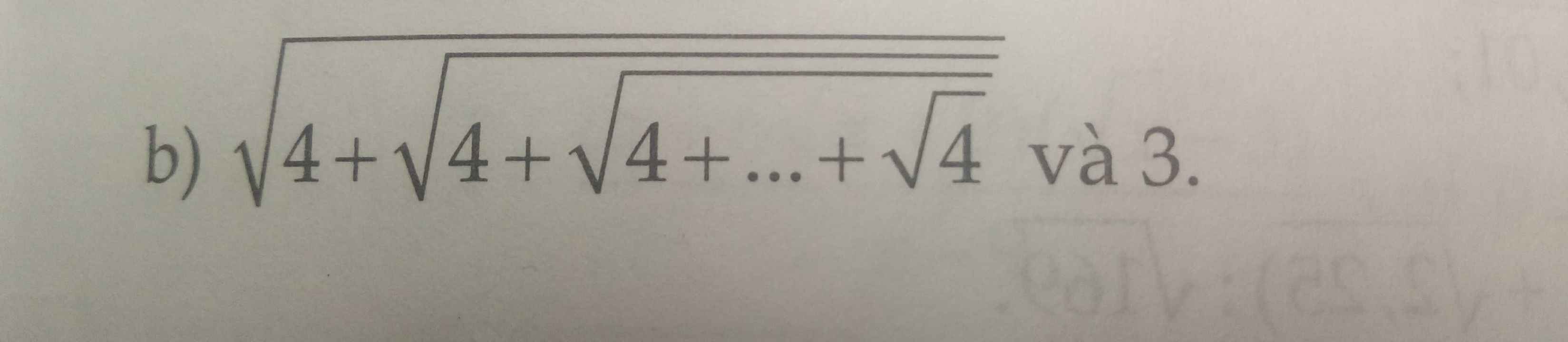K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KT
0
KV
3
7 tháng 6 2017
Bài này may mình có thi qua rùi.
Đặt
\(A=\sqrt{4+\sqrt{4+\sqrt{4+...+\sqrt{4}}}}>0\)
=> \(A^2=4+\sqrt{4+\sqrt{4+...+\sqrt{4}}}\)
=> A2 - A = 4
=> A2 - A - 4 = 0
Giải phương trình được 2 nghiệm:
\(A_1=\frac{1+\sqrt{17}}{2}\)
\(A_2=\frac{1-\sqrt{17}}{2}< 0\)( loại vì A>0)
Vậy \(A=\frac{1+\sqrt{17}}{2}< \frac{1+\sqrt{25}}{2}=\frac{1+5}{2}=3\)
Kết luận: \(\sqrt{4+\sqrt{4+\sqrt{4+...+\sqrt{4}}}}< 3\)
-------------
Chắc bạn ko hiểu chỗ A2 - A = 4 nhỉ?
L
2
26 tháng 7 2020
\(\sqrt{4+\sqrt{4+\sqrt{4+\sqrt{4+...}}}}< \sqrt{6+\sqrt{6+\sqrt{6+...\sqrt{6+\sqrt{9}}}}}\)(100 dấu căn)
=> \(VT< \sqrt{6+\sqrt{6+\sqrt{6+...\sqrt{6+3}}}}=\sqrt{6+\sqrt{6+\sqrt{6+..\sqrt{6+\sqrt{9}}}}}\)(99 dấu căn)
=> \(VT< \sqrt{6+3}=3\)
17 tháng 8 2017
Ta có:
\(\frac{1-\sqrt{n}+\sqrt{n+1}}{1+\sqrt{n}+\sqrt{n+1}}=\frac{\left(1-\sqrt{n}+\sqrt{n+1}\right)^2}{\left(1+\sqrt{n}+\sqrt{n+1}\right)\left(1-\sqrt{n}+\sqrt{n+1}\right)}=\frac{2n+2-2\sqrt{n}+2\sqrt{n+1}-2\sqrt{n\left(n+1\right)}}{2\left(1+\sqrt{n+1}\right)}\)
\(=\frac{\left[2n+2-2\sqrt{n}+2\sqrt{n+1}-2\sqrt{n\left(n+1\right)}\right]\left(1-\sqrt{n+1}\right)}{2\left(1+\sqrt{n+1}\right)\left(1-\sqrt{n+1}\right)}=\frac{-2n\sqrt{n+1}+2n\sqrt{n}}{-2n}=\sqrt{n+1}-\sqrt{n}\)
Suy ra:
\(Q=\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+...+\sqrt{2017}-\sqrt{2016}=\sqrt{2017}-\sqrt{2}< \sqrt{2017}-1=R\)
Vậy Q < R.
TN
2
K
5 tháng 7 2019
\(A=\sqrt{4+\sqrt{4+\sqrt{4+....}}}\)vô số dấu căn
\(\Leftrightarrow A^2=4+\sqrt{4+\sqrt{4+\sqrt{4+....}}}\)
\(\Leftrightarrow A^2-A-4=0\)
\(\Leftrightarrow\orbr{\begin{cases}A=\frac{1-\sqrt{17}}{2}\left(l\right)\\A=\frac{1+\sqrt{17}}{2}=2,56< 3\end{cases}}\)
Từ đây ta có \(\sqrt{4+\sqrt{4+\sqrt{4+....}}}< 3\)
5 tháng 7 2019
\(A=\sqrt{4+\sqrt{4}+\sqrt{4+.....}}\)vô số dấu căn
\(\Leftrightarrow A^2=4+\sqrt{4+\sqrt{4+\sqrt{4+...}}}\)
\(\Leftrightarrow A^2-A-A=0\)
\(\Leftrightarrow\orbr{\begin{cases}A=\frac{1-\sqrt{17}}{2}\\A=\frac{1+\sqrt{17}}{2}=2,56< 3\end{cases}}\)
Từ đây ta có: \(\sqrt{4+\sqrt{4}+\sqrt{4+.....}}< 3\)
Rất vui vì giúp đc bạn <3
T
3
20 tháng 6 2017
Bài này giải nhiều rồi. Thôi m trình bày thêm 1 lần nữa vậy. Lần sau tìm câu hỏi tương tự nha b.
Ta có:
\(A=\sqrt{4+\sqrt{4+\sqrt{4....}}}\) vô số dấu căn
\(\Leftrightarrow A^2=4+\sqrt{4+\sqrt{4+\sqrt{4....}}}\)
\(\Leftrightarrow A^2-A-4=0\)
\(\Leftrightarrow\orbr{\begin{cases}A=\frac{1-\sqrt{17}}{2}\left(l\right)\\A=\frac{1+\sqrt{17}}{2}=2,56< 3\end{cases}}\)
Từ đây ta có \(\sqrt{4+\sqrt{4+\sqrt{4....}}}< 3\)
TD
0
Bạn xem lại đề nhé. Theo mình nghĩ thì không có căn 4 ở sau dấu.... Đây là vô hạn mà.
cảm ơn phương pháp của bạn nhiều nhé, nhờ bạn mà mình làm đc rồi ^^