Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(-2< -1,75< 0< \sqrt{5}< \pi< \dfrac{22}{7}< 5\dfrac{3}{6}.\)

Bài 2 :
Giả sử \(a=\sqrt{3}\)là số hữu tỉ
Khi đó ta có \(a=\sqrt{3}=\frac{m}{n}\)với m, n tối giản ( n khác 0 )
Từ \(\sqrt{3}=\frac{m}{n}\Rightarrow m=\sqrt{3}n\)
Bình phương 2 vế ta được đẳng thức: \(m^2=3n^2\)(*)
\(\Rightarrow m^2⋮3\)mà m tối giản \(\Rightarrow m⋮3\)
=> m có dạng \(3k\)
Thay m vào (*) ta có : \(9k^2=3n^2\)
\(\Leftrightarrow3k^2=n^2\)
\(\Leftrightarrow n=\sqrt{3}k\)
Vì k là số nguyên => n không là số nguyên
=> điều giả sử là sai
=> \(\sqrt{3}\)là số vô tỉ

a: \(-3< -2.15< -\sqrt{3}< 0< \dfrac{13}{7}< \sqrt{8}< \dfrac{33}{12}\)
b: \(0< \sqrt{3}< \dfrac{13}{7}< 2.15< \dfrac{33}{12}< \sqrt{8}< 3\)

a)-3<-2<-\(\sqrt[]{3}\)<0<\(\dfrac{13}{7}\)<\(\dfrac{33}{12}\)<\(\sqrt{8}\)<15
b)|0|<|-\(\sqrt{3}\)|\(\dfrac{13}{7}\)|<|-2|<|\(\dfrac{33}{12}\)|<\(\sqrt{8}\)<|-3|<15

\(\sqrt{484}-\dfrac{1}{\sqrt{5}}< \sqrt{529}-\dfrac{1}{19}< \sqrt{576}-\dfrac{1}{\sqrt{7}}< \sqrt{625}-\dfrac{1}{\sqrt{8}}\)

Lời giải:
Viết các phân số dưới dạng tối giản:
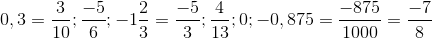
- So sánh các số hữu tỉ dương với nhau:
Ta có : 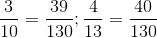
Vì 39 < 40 và 130 > 0 nên 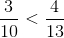
- Tương tự So sánh các số hữu tỉ âm với nhau
Vậy: 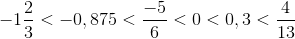
Bài 22 Sắp xếp các số hữu tỉ sau theo thứ tự lớn dần:
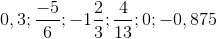
Lời giải:
Viết các phân số dưới dạng tối giản:
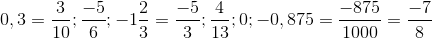
- So sánh các số hữu tỉ dương với nhau:
Ta có : 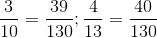
Vì 39 < 40 và 130 > 0 nên 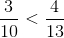
- Tương tự So sánh các số hữu tỉ âm với nhau
Vậy: 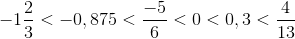
\(\sqrt{16}=4;\dfrac{2}{3}=0,\left(6\right);\Omega=3,14;-\sqrt{5}\simeq-2,24\)
\(-5,6< -2,23< 0\)
=>\(-5,6< -\sqrt{5}< 0\)(1)
\(0< \dfrac{2}{3}< 3,14< 4\)
=>\(0< \dfrac{2}{3}< \Omega< \sqrt{16}\)(2)
Từ (1) và (2) suy ra \(-5,6< -\sqrt{5}< 0< \dfrac{2}{3}< \Omega< \sqrt{16}\)