Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mặt đáy: \(ABCD\)
Các mặt bên: \(IAD\); \(IAB\); \(IBC\); \(ICD\)
b) Các cạnh bên bằng nhau: \(IB = IC = 18\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 14\)cm
c) Đoạn thẳng \(IH\) là đường cao của hình chóp

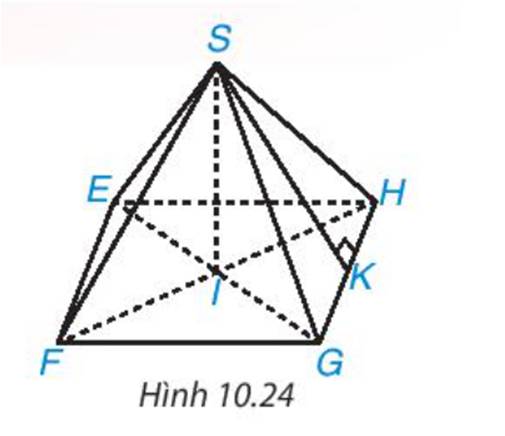
- Đỉnh: S
- Cạnh bên: SE, SF, SG, SH
- Mặt bên: SEF, SFG, SGH. SEH
- Mặt đáy: EFGH
- Đường cao: SI
- Một trung đoạn: SK

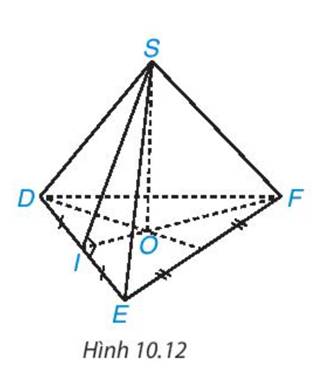
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: SDE, SEF, SDF
- Mặt đáy: DEF
- Đường cao: SO
- Một trung đoạn: SI

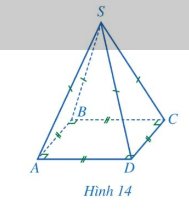
Hình chóp tứ giác đều S.ABCD có:
- Mặt đáy ABCD là hình vuông.
- Các mặt bên là SAB, SBC, SCD, SDA là những tam giác cân tại S.
- Các cạnh đáy AB, BC, CD, DA bằng nhau.
- Các cạnh bên SA, SB, SC, SD bằng nhau.
- S gọi là đỉnh của hình chóp đều S. ABCD

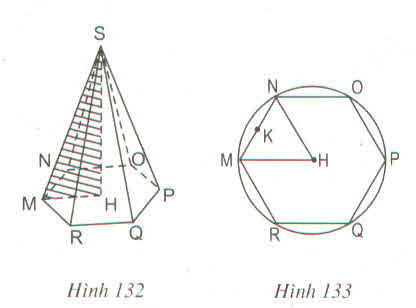
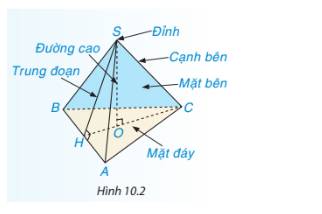
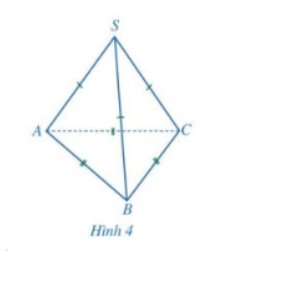
Hình chóp tam giác đều S. ABC có:
- Đỉnh: S
- Cạnh bên: SA, SB, SC.
- Mặt đáy: tam giác ABC.
- Đường cao: SO.
- Trung đoạn: SH

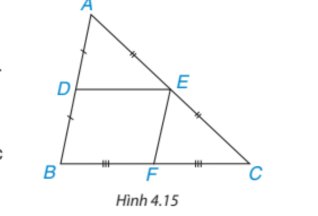
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

Hình chóp tam giác đều S. ABCD có:
- Mặt đáy: ABC là một tam giác đều
- Các mặt bên SAB, SBC, SCA là những tam giác cân tại S.
- Các cạnh đáy: AB, BC, CA bằng nhau.
- Các cạnh bên; SA, SB, SC, SD
- S gọi là đỉnh của hình chóp tam giác đều S. ABC
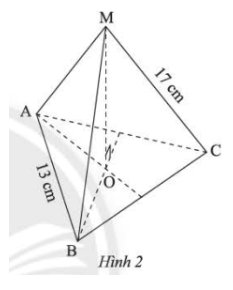


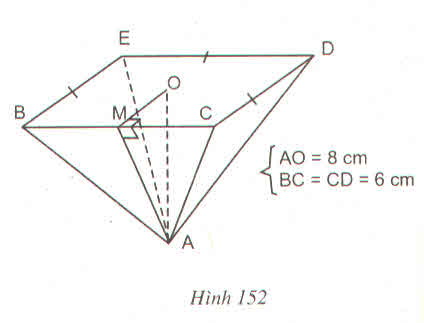

a) Đỉnh: \(M\)
Mặt đáy: \(ABC\)
Các mặt bên: \(MAB\); \(MAC\); \(MBC\)
b) Các cạnh bên bằng nhau: \(MA = MC = 17\)cm
Các cạnh đáy bằng nhau: \(BC = AB = 13\)cm
c) Đoạn thẳng \(MO\) là đường cao của hình chóp tam giác đều \(M.ABC\)