Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Có 1 đường duy nhất
b: Đường thẳng d cắt (P) tại 1 giao điểm

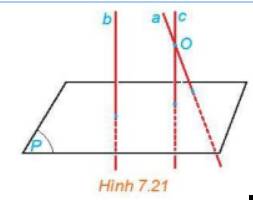
a) b // c; b ⊥ (P) ⇒ c ⊥ (P)
Mà a ⊥ (P)
a, c cùng đi qua điểm O
⇒ a trùng c.
b) Ta có b // c mà a trùng c nên a // b.

Khẳng định (1) đúng vì khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Khẳng định (2) sai vì qua một điểm có vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Khẳng định (3) sai vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Khẳng định (4) sai vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.
Vậy có một khẳng định đúng.
ĐÁP ÁN A

Tham khảo:
a) 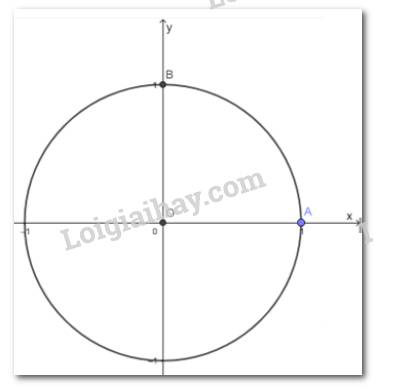
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
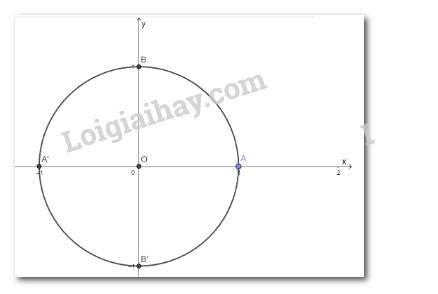

Câu a) đúng. Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c). Tính chất của khoảng cách giữa hai đường thẳng chéo nhau (Bài 5 – chương III).
Câu b) sai. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai. Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước. Để có khẳng định đúng ta phải nói: Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho.
Câu d) sai. Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường ấy.

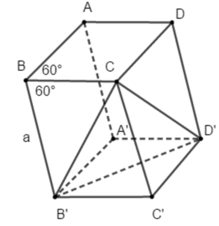
Phương án A, B và D đều sai
Phương án C đúng vì tam giác CB’D’ có ba cạnh bằng a, a√3,a√3 nên không thể vuông tại B’
Đáp án C
a,5 đường thẳng cắt nhau tại 1 điểm tạo thành 10 tia chung gốc
Mỗi tia tạo với 9 tia còn lại thành 9 góc mà có 10 tia như vậy tì số góc được tạo thành là :
9 . 10 = 90 ( góc )
Vì mỗi góc được lặp lại 2 lần nên có tất cả :
90 : 2 = 45 ( góc )
b, 5 đường thẳng cắt nhau tạo thành 5 góc bẹt . Vậy có tất cả :
45 - 5 = 40 góc khác góc bẹt
Có 40 góc khác góc bẹt mà mỗi góc có 1 góc đối đỉnh với nó nên có tất cả :
40 : 2 = 20 ( cặp góc đối đỉnh )
c, 5 đường thẳng cắt nhau tạo thành 10 góc không có điểm chung
\(\Rightarrow\) Tổng 10 góc này là 360 độ
\(\Rightarrow\) Tổng của 10 góc này nhỏ hơn 360 độ ( vô lý )
\(\Rightarrow\) Trong 10 góc này tồn tại ít nhất 1 góc lớn hơn 36 độ
\(\Rightarrow\) Tổng của 10 góc này lớn hơn 360 độ ( vô lý )
\(\Rightarrow\) Trong 10 góc này tồn tại ít nhất 1 góc nhỏ hơn hoặc = 36 độ
a) Năm đường thẳng cắt nhau tại 1 điểm tạo thành 10 tia chung gốc.
Mỗi tia tạo với 9 tia còn lại 9 góc mà có 10 tia như vậy nên có tất cả số góc là:
9 x 10 = 90 ( góc )
Vì mỗi góc được tính lặp lại 2 lần nên:
90 : 2 = 45 ( góc )
b) 5 đường thẳng cắt nhau tạo thành 5 góc bẹt. Vậy có tất cả số góc khác góc bẹt là:
45 - 5 = 40 ( góc khác góc bẹt )
Có tất cả 40 góc khác góc bẹt mà mỗi góc có 1 góc đối đỉnh với nó. Nên có tất cả :
40 : 2 = 20 ( cặp góc đối đỉnh )
c) Năm đường thẳng cắt nhau tạo thành 10 góc không có điểm trong chung.
=> Tổng của 10 góc này bằng 360o
Giả sử cả 10 góc đều bé hơn 36o
=> Tổng của 10 góc này < 360o ( điều này là vô lý )
=> Trong 10 góc này tồn tại ít nhất 1 góc nhỏ hơn 36o