K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 11 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}1-4m=-\dfrac{1}{2}\\m-2\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{8}\\m\ne5\end{matrix}\right.\Leftrightarrow m=\dfrac{3}{8}\\ b,\Leftrightarrow1-4m>0\Leftrightarrow m< \dfrac{1}{4}\\ c,\Leftrightarrow x=\dfrac{1}{2};y=0\Leftrightarrow\dfrac{1}{2}\left(1-4m\right)=2-m\Leftrightarrow1-4m=4-2m\\ \Leftrightarrow m=-\dfrac{3}{2}\)
T
13 tháng 9 2023
\(\dfrac{3}{2\sqrt{2}-3\sqrt{3}}-\dfrac{3}{2\sqrt{2}+3\sqrt{3}}\)
\(=\dfrac{3\left(2\sqrt{2}+3\sqrt{3}\right)}{\left(2\sqrt{2}-3\sqrt{3}\right)\left(2\sqrt{2}+3\sqrt{3}\right)}-\dfrac{3\left(2\sqrt{2}-3\sqrt{3}\right)}{\left(2\sqrt{2}-3\sqrt{3}\right)\left(2\sqrt{2}+3\sqrt{3}\right)}\)
\(=\dfrac{3\left(2\sqrt{2}+3\sqrt{3}-2\sqrt{2}+3\sqrt{3}\right)}{\left(2\sqrt{2}-3\sqrt{3}\right)\left(2\sqrt{2}+3\sqrt{3}\right)}\)
\(=\dfrac{3\cdot6\sqrt{3}}{\left(2\sqrt{2}\right)^2-\left(3\sqrt{3}\right)^2}\)
\(=\dfrac{18\sqrt{3}}{8-27}\)
\(=-\dfrac{18\sqrt{3}}{19}\)
#Toru
BL
4
1 tháng 11 2020
\(\sqrt{5-2\sqrt{2+\sqrt{9+4\sqrt{2}}}}\)
= \(\sqrt{5-2\sqrt{2+\sqrt{8+4\sqrt{2}+1}}}\)
= \(\sqrt{5-2\sqrt{2+\sqrt{\left(\sqrt{8}+1\right)^2}}}\)
= \(\sqrt{5-2\sqrt{2+2\sqrt{2}+1}}\)
= \(\sqrt{5-2\sqrt{\left(\sqrt{2}+1\right)^2}}\)
= \(\sqrt{5-2\left(\sqrt{2}+1\right)}\)
= \(\sqrt{5-2\sqrt{2}-2}\)
= \(\sqrt{\left(\sqrt{2}-1\right)^2}\)
= \(\sqrt{2}-1\)
K
1
31 tháng 8 2020
ĐKXĐ:\(x>-3\)
\(\sqrt{x}+\sqrt{x+3}=x+4\)\(\Leftrightarrow x+x+3+2\sqrt{x}\sqrt{x+3}=\left(x+4\right)^2\)
\(\Leftrightarrow2x+3+2\sqrt{x^2+3x}=x^2+8x+16\)
\(\Leftrightarrow x^2+8x+16-2x-3-2\sqrt{x^2+3x}=0\)
\(\Leftrightarrow\left(x^2+3x-2\sqrt{x^2+3x}+1\right)+3x+12=0\)
\(\Leftrightarrow\left(\sqrt{x^2+3x}-1\right)^2+3\left(x+4\right)=0\)
Ta thấy:\(\hept{\begin{cases}\left(\sqrt{x^2+3x}-1\right)^2\ge0\\x>-3\Leftrightarrow3\left(x+4\right)>0\end{cases}}\)
\(\Rightarrow\left(\sqrt{x^2+3x}-1\right)^2+3\left(x+4\right)>0\)
\(\Leftrightarrow x\in\varnothing\)
Vậy phương trình vô nghiệm.
7 tháng 4 2019
n>4 nữa nha bạn
Ta có:\(A=n^4-4n^3-4n^2+16n\)
\(=\left(n^4-4n^3\right)-\left(4n^2-16n\right)\)
\(=n^3\left(n-4\right)-4n\left(n-4\right)\)
\(=\left(n-4\right)\left(n^3-4n\right)\)
\(=n\left(n-3\right)\left(n^2-4\right)\)
\(=n\left(n-2\right)\left(n+2\right)\left(n-4\right)\)
Do n là số chẵn và n>4 nên đặt \(n=2k+2\left(k>1\right)\).
\(\Rightarrow A=\left(2k+2\right)\left(2k+4\right)\left(2k-2\right)2k\)
\(=16k\left(k-1\right)\left(k+1\right)\left(k+2\right)\)
\(=16\left(k-1\right)k\left(k+1\right)\left(k+2\right)\)
Do \(\left(k-1\right)k\left(k+1\right)\left(k+2\right)\) là tích 4 số nguyên dương liên tiếp nên chúng chia hết cho 2.3.4=24
Vậy A chia hết cho 16*24=384(đpcm)
BH
28 tháng 7 2019
\(B=\frac{1}{-\left(x-2\sqrt{x}+1\right)-2}=\frac{1}{-\left(\sqrt{x}-1\right)^2-2}\)
\(\left(\sqrt{x}-1\right)^2\ge0\Leftrightarrow-\left(\sqrt{x}-1\right)^2\le0\)
\(\Leftrightarrow-\left(\sqrt{x}-1\right)^2-2\le-2\)
\(\Leftrightarrow\frac{1}{-\left(\sqrt{x}-1\right)^2-2}\ge\frac{1}{-2}=\frac{-1}{2}\)
\("="\Leftrightarrow x=1\)
Vậy biểu thức B đạt giá trị nhỏ nhất là -1/2 khi x=1
NM
2
6 tháng 3 2022
a: Thay x=0 và y=5 vào (d), ta được:
(m-2)x0+m=5
=>m=5
c: Để hai đườg song song thì m-2=2
hay m=4
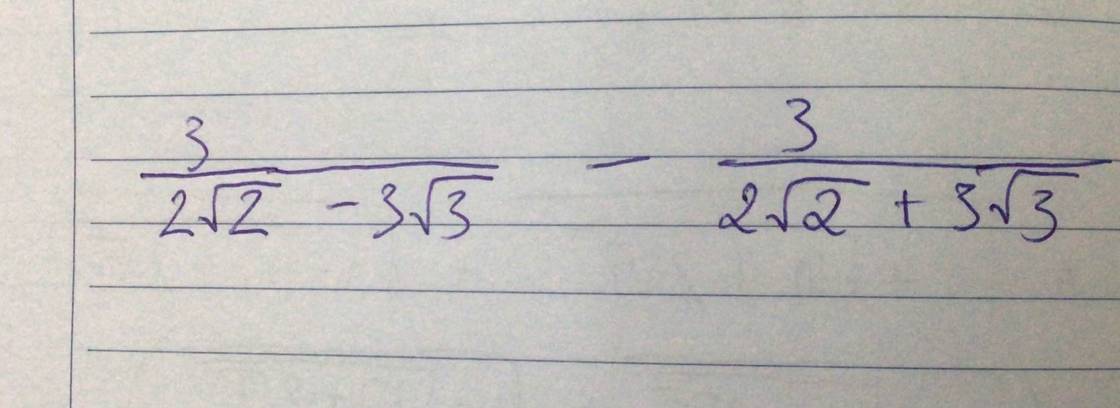
ĐK : \(2x^4-8x^2+16=2\left(x^4-4x^2+8\right)=2\left(x^2-2\right)^2+8>0\)
\(\Leftrightarrow2x^4-8x^2+16=8\Leftrightarrow2x^4-8x^2+8=0\)
\(\Leftrightarrow x^4-4x^2+4=0\Leftrightarrow\left(x^2-2\right)^2=0\Leftrightarrow x=\pm2\)