K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 10 2021
\(5\sqrt{\dfrac{1}{2}}+\dfrac{1}{2}\sqrt{20}+\sqrt{5}\)
\(=\dfrac{5\sqrt{2}}{2}+\sqrt{5}+\sqrt{5}=\dfrac{5\sqrt{2}}{2}+2\sqrt{5}\)
\(=\dfrac{5\sqrt{2}}{2}+\dfrac{4\sqrt{5}}{2}=\dfrac{5\sqrt{2}+4\sqrt{5}}{2}\)
21 tháng 10 2021
\(5\sqrt{\dfrac{1}{2}}+\dfrac{1}{2}\sqrt{20}+\sqrt{5}=\dfrac{5}{\sqrt{2}}+\dfrac{\sqrt{20}}{2}+\sqrt{5}=\dfrac{5\sqrt{2}+\sqrt{20}}{2}+\sqrt{5}=\dfrac{\sqrt{50}+\sqrt{20}}{\sqrt{4}}+\sqrt{5}=\dfrac{\sqrt{10}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{4}}+\sqrt{5}=\dfrac{\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{2}}+\sqrt{5}=\dfrac{5+\sqrt{10}+\sqrt{10}}{\sqrt{2}}=\dfrac{5+2\sqrt{10}}{\sqrt{2}}\)
LN
19 tháng 7 2021
\(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\\ =\dfrac{2-\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\dfrac{2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\\ =\dfrac{2-\sqrt{3}+2+\sqrt{3}}{2^2-\left(\sqrt{3}\right)^2}\\ =\dfrac{2+2}{4-3}\\ =4\)
19 tháng 7 2021
Ta có: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=2-\sqrt{3}+2+\sqrt{3}\)
=4
2
21 tháng 5 2023
`(4\sqrt{6}+x)^2=8^2+(6+\sqrt{x^2+4})^2`
`<=>96+8\sqrt{6}x+x^2=64+36+12\sqrt{x^2+4}+x^2+4`
`<=>2\sqrt{6}x-2=3\sqrt{x^2+4}` `ĐK: x >= \sqrt{6}/6`
`<=>24x^2-8\sqrt{6}x+4=9x^2+36`
`<=>15x^2-8\sqrt{6}x-32=0`
`<=>x^2-[8\sqrt{6}]/15x-32/15=0`
`<=>(x-[4\sqrt{6}]/15)^2-64/25=0`
`<=>|x-[4\sqrt{6}]/15|=8/5`
`<=>[(x=[24+4\sqrt{6}]/15 (t//m)),(x=[-24+4\sqrt{6}]/15(ko t//m)):}`
HT
0
S2
1
20 tháng 5 2022
\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Giải pt chứa nhiều dấu trị tuyệt đối thì cần xét các khoảng giá trị.
Để xét các khoảng giá trị, ta căn cứ vào xét các khoảng mà tại đó dấu trị tuyệt đối có thể phá.
Ví dụ: Ta biết $|x-a|=x-a$ nếu $x\geq a$ và $a-x$ nếu $x< a$
Do đó, khi gặp phải pt:
$|x-1|+|x+1|=3x-5$ chả hạn. Ta thấy:
$|x-1|=x-1$ nếu $x\geq 1$ và $1-x$ nếu $x< 1$
$|x+1|=x+1$ nếu $x\geq -1$ và $-x-1$ nếu $x< -1$
Như vậy, kết hợp cả 2 điều trên thì ta xét các khoảng sau:
TH1: $x\geq 1$
TH2: $-1\leq x< 1$
TH3: $x< -1$
TN
1
MH
27 tháng 4 2022
Ta có:
\(x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=4\)
\(\left(x^2-2+\dfrac{1}{x^2}\right)+\left(y^2-2+\dfrac{1}{y^2}\right)+4=4\)
\(\left(x-\dfrac{1}{x}\right)^2+\left(y-\dfrac{1}{y}\right)^2=0\)
Vì \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{x}\right)^2\ge0\forall x\\\left(y-\dfrac{1}{y}\right)\ge0\forall y\end{matrix}\right.\)
Dấu "="⇔ \(\left\{{}\begin{matrix}x=\dfrac{1}{x}\\y=\dfrac{1}{y}\end{matrix}\right.\)
\(\Leftrightarrow x^2=y^2=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\x=y=-1\\x=1,y=-1\\x=-1,y=1\end{matrix}\right.\)
Thay vào phương trình 1
⇒ \(x=y=1\)
8 tháng 12 2023
Câu 1:
1:
a: \(\dfrac{1}{2}x-3=0\)
=>\(\dfrac{1}{2}x=3\)
=>\(x=3:\dfrac{1}{2}=3\cdot2=6\)
b: \(3x^2-12x=0\)
=>\(3x\cdot x-3x\cdot4=0\)
=>\(3x\left(x-4\right)=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
2:
a: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=-x+\dfrac{3}{2}\)
=>\(x^2=-2x+3\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Khi x=-3 thì \(y=\dfrac{1}{2}\cdot\left(-3\right)^2=\dfrac{1}{2}\cdot9=4,5\)
Khi x=1 thì \(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)
b: Gọi (d1): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Thay x=2 và y=2 vào (d), ta được:
\(a\cdot2+b=2\)
=>2a+b=2
=>b=2-2a
=>y=ax+2-2a
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=ax+2-2a\)
=>\(\dfrac{1}{2}x^2-ax-2+2a=0\)
\(\text{Δ}=\left(-a\right)^2-4\cdot\dfrac{1}{2}\cdot\left(2a-2\right)\)
\(=a^2-2\left(2a-2\right)=a^2-4a+4=\left(a-2\right)^2\)
Để (P) tiếp xúc với (d1) thì Δ=0
=>a-2=0
=>a=2
=>b=2-2a=2-4=-2
Vậy: Phương trình đường thẳng cần tìm là y=2x-2
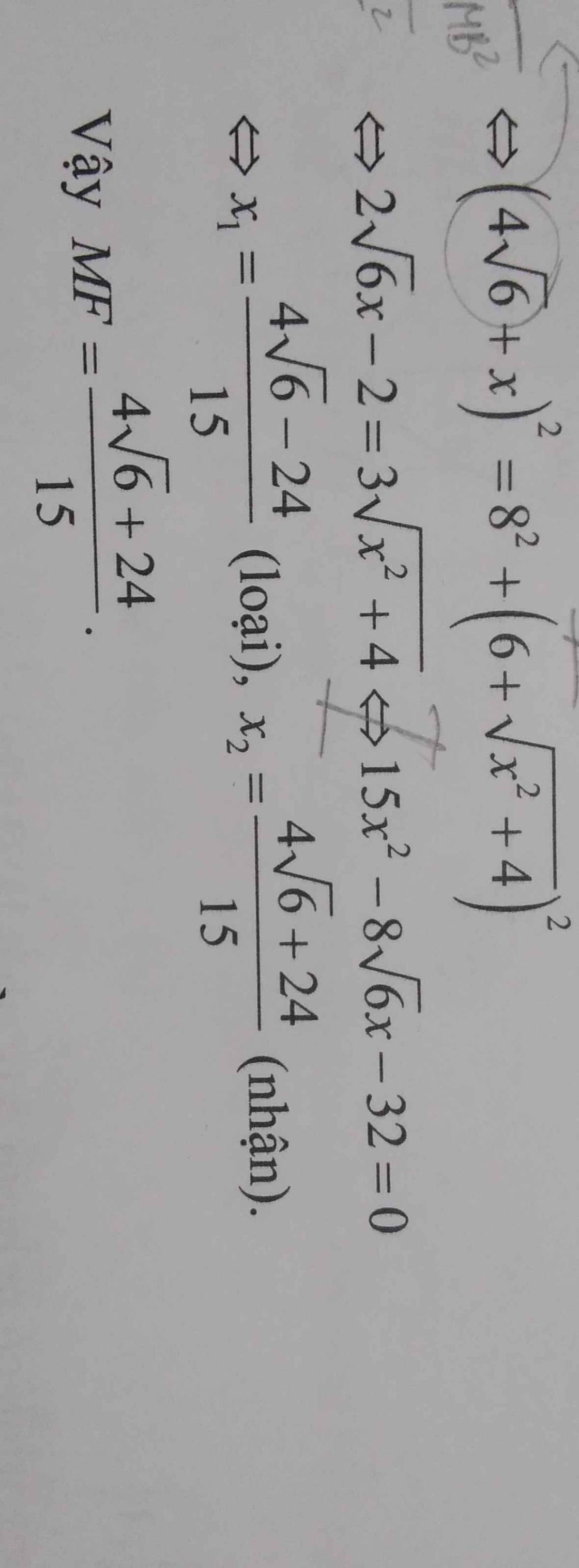
Nhìn trên hình bạn có thể thấy rõ các điểm đó là điểm (-1;1) và (2;4)
Nhưng trong trường hợp đề không cho hình thì ta làm như sau:
Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=x+2\)\(\Leftrightarrow x^2-x-2=0\)(*)
Xét pt (*) có \(\Delta=\left(-1\right)^2-4.1.\left(-2\right)=9>0\)
Vậy pt (*) có 2 nghiệm phân biệt \(\orbr{\begin{cases}x_1=\frac{-\left(-1\right)+\sqrt{9}}{2.1}=2\\x_2=\frac{-\left(-1\right)-\sqrt{9}}{2.1}=-1\end{cases}}\)
Khi \(x=2\Rightarrow y=x+2=2+2=4\)
Khi \(x=-1\Rightarrow y=x+2=-1+2=1\)
Vậy ta tìm được đúng các điểm (-1;1) và (2;4)