


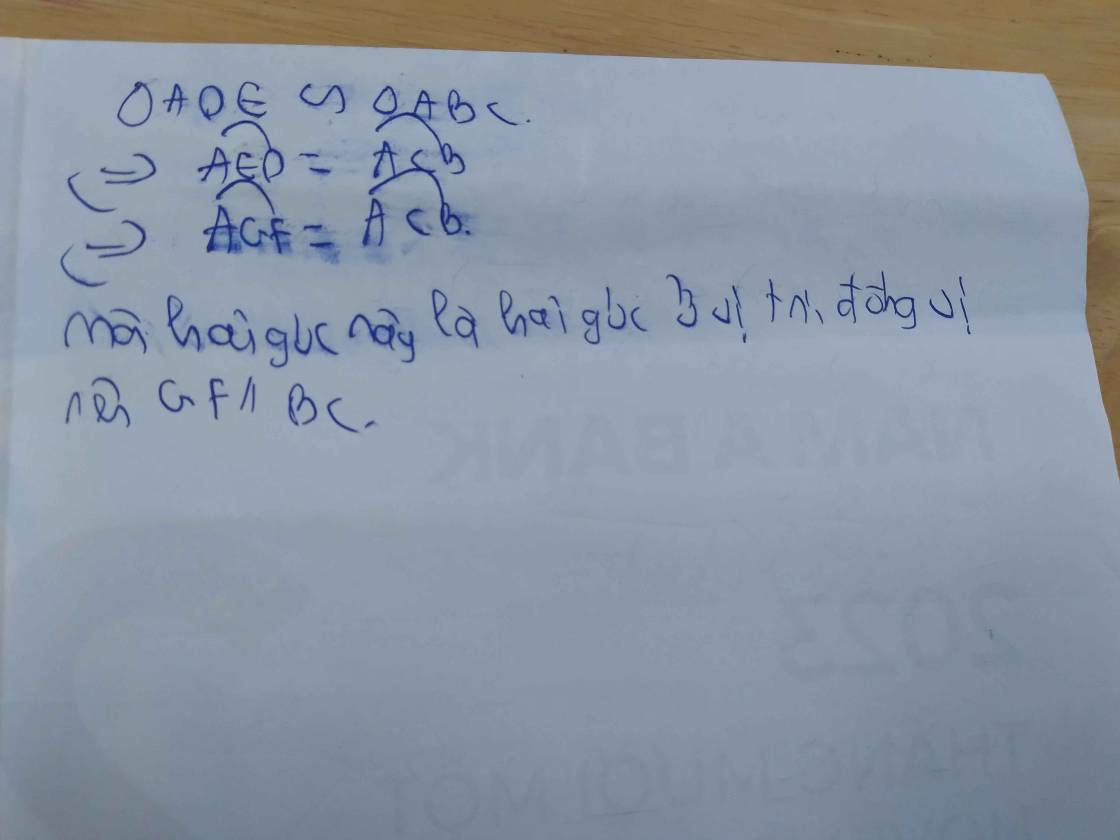
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




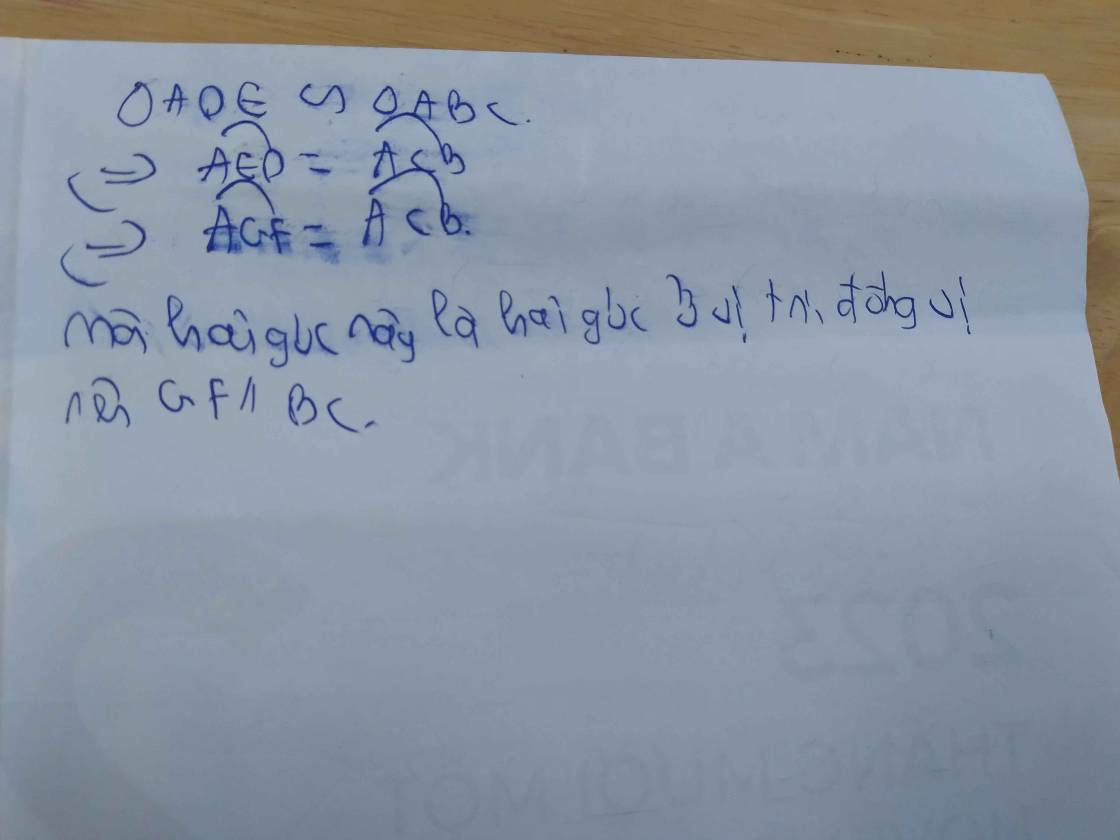

Hình (tự vẽ)
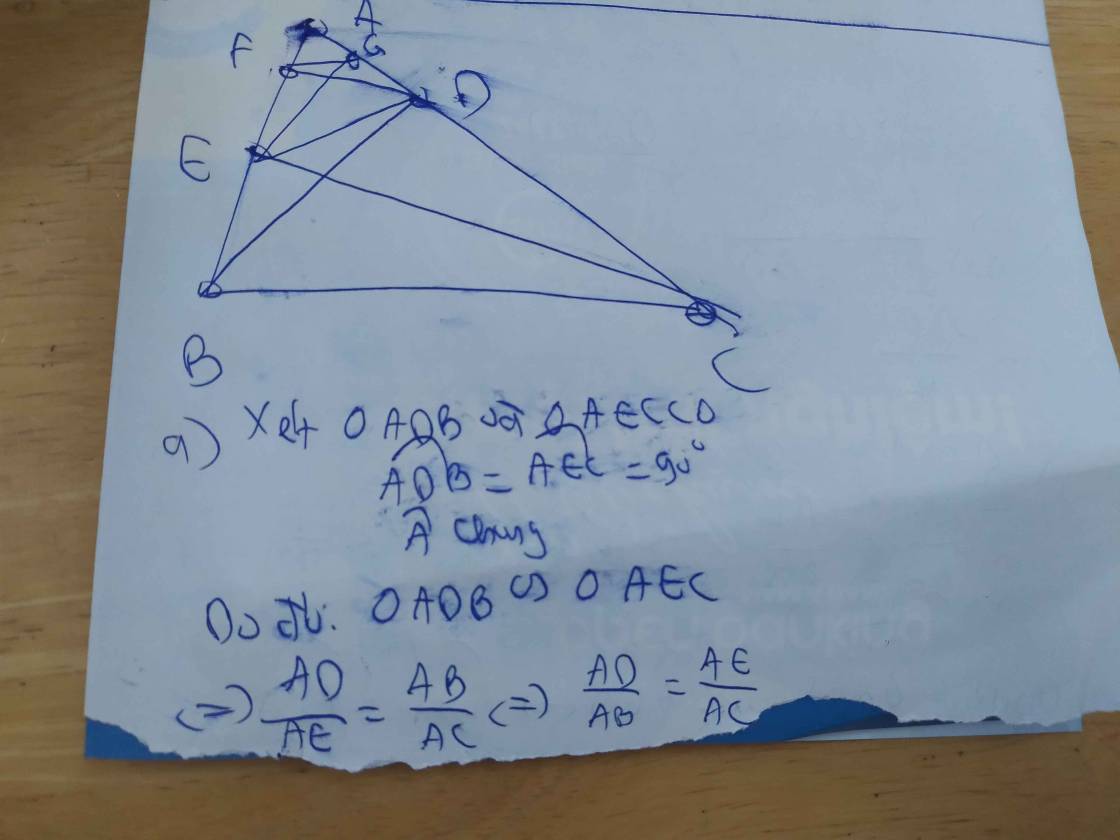
a) Xét \(\Delta ABDva\Delta ACE\):
\(\widehat{A}\left(chung\right)\)
\(\widehat{E}=\widehat{D}\left(=90'\right)\)
\(=>\Delta ABD\)đồng dạng \(\Delta ACE\left(g-g\right)\)
\(=>\frac{AB}{AC}=\frac{AD}{AE}< =>AB.AE=AC.AD\)
b)xét \(\Delta ADEva\Delta ABC\)
\(\widehat{A}\left(chung\right)\)
\(\frac{AB}{AC}=\frac{AD}{AE}\)
\(=>\Delta ADE\)đồng dạng \(\Delta ABC\left(c-g-c\right)\)
c)Lưu Ý! Đề phải là DE cắt CB tại I
CM:
\(\widehat{IEB}=\widehat{AED}\)(đối đỉnh)
\(\widehat{AED}=\widehat{ACB}\)(tam giác ADE đồng dạng với tam giác ABC)
\(=>\widehat{IEB}=\widehat{ACB}\)
Lại có góc I chung
\(=>\Delta IBE\) đồng dạng với \(\Delta IDC\left(g-g\right)\)
d) từ c)=>\(\frac{IB}{ID}=\frac{IE}{IC}< =>ID.IE=IB.IC=\left(OI-OB\right)\left(OI+OC\right)\)
Mà OC=OB(gt)
\(=>ID.IE=\left(OI+OC\right)\left(OI-OC\right)=OI^2-OC^2\)

Lời giải:
a)
Xét tam giác $ABD$ và $ACE$ có:
\(\widehat{A}\) chung
\(\widehat{ADB}=\widehat{AEC}=90^0\)
\(\Rightarrow \triangle ABD\sim \triangle ACE(g.g)\Rightarrow \frac{AB}{AD}=\frac{AC}{AE}\) hay \(\frac{AD}{AE}=\frac{AB}{AC}\)
Xét tam giác $ADE$ và $ABC$ có:
\(\widehat{A}\) chung
\(\frac{AD}{AE}=\frac{AB}{AC}\) (cmt)
\(\Rightarrow \triangle ADE\sim \triangle ABC(c.g.c)\)
b)
\(EG\perp AC; BD\perp AC\Rightarrow EG\parallel BD\)
\(DF\perp AB, CE\perp AB\Rightarrow DF\parallel CE\)
Do đó áp dụng định lý Ta-let ta có:
\(\left\{\begin{matrix} \frac{AG}{AD}=\frac{AE}{AB}\\ \frac{AF}{AE}=\frac{AD}{AC}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} AG=\frac{AE.AD}{AB}\\ AF=\frac{AD.AE}{AC}\end{matrix}\right.\)
\(\Rightarrow \frac{AG}{AF}=\frac{AC}{AB}\Rightarrow \frac{AG}{AC}=\frac{AF}{AB}\). Theo định lý Ta-let đảo suy ra \(FG\parallel BC\) (đpcm)

Xét tg ABD vuông tại D và tg ACE vuông tại E
có: ^A chung
=> tg ABD ~ tg ACE (gn)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\Rightarrow\frac{AD}{AB}=\frac{AE}{AC}\)
xét tg ADE và tg ABC
có: AD/AB = AE/AC (cmt)
^A chung
=> tg ADE ~ tg ABC (c-g-c)
hình bn tự kẻ nha