Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trả lời:
P/s Nghĩ gì làm đấy nên hông chắc à nha!!! (^-^)
b)Xét tam giác AEC và tam giác ADB, có:
+ Góc AEC = góc ADB (Giả thiết)
+ Góc A chung
=> tam giác AEC đồng dạng với tam giác ADB (G-G)
a) Ta có: AE/AB=AD/AC;AB/AC=ED/BC (VÌ tam giác AEC đồng dạng với tam giác ADB ở chứng minh trên)
=> ED//BC
+) Xét tam giác AED và tam giác ABC, có:
+ AED = ABC ( hai góc đồng dạng do ED//BC)
+ Góc A chung
=> Tam giác AED đồng dạng với tam giác ABC (G-G)
=> AE/AB = AD/AC ( Tính chất )
=> AB.AC = AD.AE ( đpcm )
~Học tốt!~
Trả lời;
P/s: Ko bik có đúng ko!!!
Ta có: MD/ME = NE/ND (VÌ tam giác AEC đồng dạng với tam giác ADB ở chứng minh trên)
=> ED//BC
+) Xét tam giác AED và tam giác ABC, có:
+ AED = ABC ( hai góc đồng dạng do ED//BC)
+ Góc A chung
=> Tam giác AED đồng dạng với tam giác ABC (G-G)
=> MD/ME = NE/ND ( Tính chất )
=> MD.NE = ME.ND ( đpcm )
~Học tốt!~
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E co
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB; AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
a, theo định lý pitago tính đc BC
sau đó xét tam giác đồng dạng ABH và CBA là tìm đc AH
hok tốt
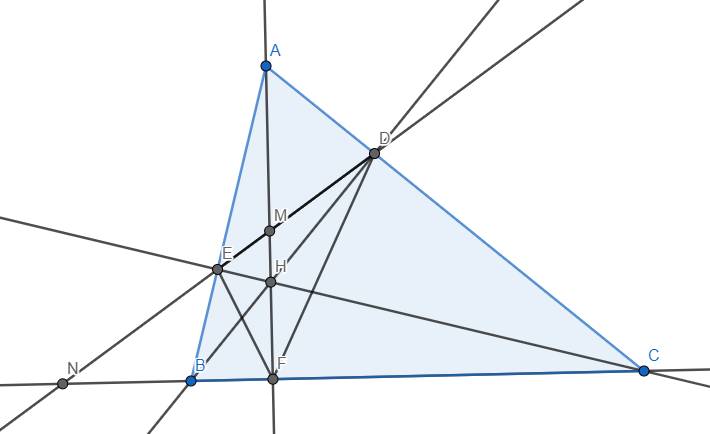
a) Xét \(\Delta ABD\) và \(\Delta ACE\), ta có \(\widehat{ADB}=\widehat{AEC}\left(=90^o\right)\) và góc A chung \(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrowđpcm\)
b) Từ \(AE.AB=AD.AC\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ADE\) và \(\Delta ABC\), ta có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) và góc A chung \(\Rightarrowđpcm\)
c) Do \(\Delta ADE~\Delta ABC\) \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2\)
Lại có \(\dfrac{AD}{AB}=cosA=cos45^o=\dfrac{1}{\sqrt{2}}\) nên \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)\(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}-S_{ADE}}=\dfrac{1}{2-1}\) \(\Rightarrow\dfrac{S_{ADE}}{S_{BEDC}}=1\)
d) Kẻ đường cao AF của tam giác ABC. Tương tự câu b, ta chứng minh được các tam giác BFE và CDF cùng đồng dạng với tam giác ABC. Từ đó suy ra \(\Delta BEF~\Delta DCF\) \(\Rightarrow\widehat{BFE}=\widehat{CFD}\) \(\Rightarrow90^o-\widehat{BFE}=90^o-\widehat{CFD}\) \(\Rightarrow\widehat{EFM}=\widehat{DFM}\) \(\Rightarrow\) FM là tia phân giác trong tam giác DEF \(\Rightarrow\dfrac{MD}{ME}=\dfrac{FD}{FE}\).
Mặt khác, \(FN\perp FM\) \(\Rightarrow\) FN là phân giác ngoài của tam giác DEF \(\Rightarrow\dfrac{ND}{NE}=\dfrac{FD}{FE}\). Từ đó suy ra \(\dfrac{MD}{ME}=\dfrac{ND}{NE}\) \(\Rightarrowđpcm\)
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc A chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC