Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta mắc hai cực của pin với một vôn kế có điện trở rất lớn thì số chỉ của vôn kế gần đúng bằng E..
- Thực hiện thí nghiệm lần lượt với hai pin, các em thu được số chỉ vôn kế và so sánh với giá trị ghi trên pin sẽ thấy số chỉ vôn kế gần đúng bằng E..

Tham khảo:
Áp dụng biểu thức hiệu điện thế của đoạn mạch chứa nguồn điện và định luật Ohm đối với toàn mạch để xác định suất điện động và điện trở trong của một pin điện hóa.
Sử dụng các đồng hồ đo điện vạn năng để đo các đại lượng trong mạch điện (đo U và I).

a. Từ
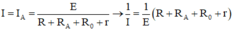
Đặt:
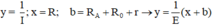
b. Căn cứ các giá trị của R và I trong phương án 1, ta tính các giá trị tương ứng của x và y.
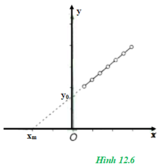
c. Vẽ đồ thị y = f (x) biểu diễn gián tiếp mối liên hệ giữa I và R.
d. Xác định tọa độ của xm và y0 là các điểm mà đồ thị trên cắt trục hoành và trục tung.
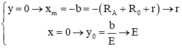

Vẽ mạch điện:
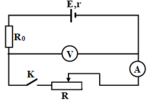
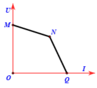
Thực hiện đo các giá trị U và I tương ứng khi thay đổi R. Vẽ đồ thị mô tả mối quan hệ đó, tức U = f(I). Áp dụng phương pháp xử lí kết quả đo được bằng đồ thị, ta vẽ được đường biểu diễn. Ở đây dự đoán là một đường thẳng có dạng y = ax + b. Đường thẳng này sẽ cắt trục tung tại U0 và cắt trục hoành tại Im. Xác định giá trị của U0 và Im trên các trục. Đồ thị vẽ được có dạng như hình sau:
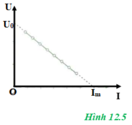
Theo phương trình đồ thị, dựa vào công thức của định luật ôm cho toàn mạch
ta có: U = E – I.(R0 + r)
Khi I = 0 ⇒ U0 = E
Khi 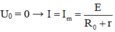
Từ đó ta tính được E và 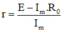

Đáp án B
+ Thí nghiệm xác định suất điện động và điện trở trong của pin điện hóa dùng đến điện trở bảo vệ, pin điện hóa và biến trở

Học sinh tự thực hiện thí nghiệm và tham khảo bảng kết quả mẫu dưới đây
Bảng 4.1. Kết quả thí nghiệm sóng dừng trên dây
Chiều dài dây AB = 1,2 m | |||
Số bụng sóng | 2 | 3 | 4 |
f (Hz) | 10 | 15 | 20 |
Nhận xét: Tần số trên dây tỉ lệ thuận với số bụng sóng.

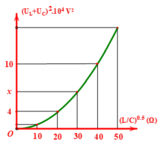
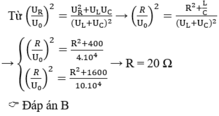


1. Dạng đồ thị và mối quan hệ U và I đối với pin cũ và pin mới là dạng đồ thị của hàm số bậc nhất nghịch biến, mối quan hệ giữa U và I là tỉ lệ nghịch với nhau.
2. Có thể sử dụng phương án:
a. Từ \(I = {I_A} = \frac{E}{{R + {R_A} + {R_0} + r}} \Rightarrow \frac{1}{I} = \frac{1}{E}\left( {R + {R_A} + {R_0} + r} \right)\)
đặt y = \(\frac{1}{x}\); x = R; b = RA + R0 + r ⇒ y = \(\frac{1}{E}\left( {x + b} \right)\)
b. Căn cứ các giá trị của R và I trong phương án 1, ta tính các giá trị tương ứng của x và y.
c. Vẽ đồ thị y = f (x) biểu diễn gián tiếp mối liên hệ giữa I và R.
d. Xác định tọa độ của xm và y0 là các điểm mà đồ thị trên cắt trục hoành và trục tung.
\(\left\{ \begin{array}{l}y = 0 \to {x_m} = - b = - \left( {{R_A} + {R_0} + r} \right) \to r\\x = 0 \to {y_0} = \frac{b}{E} \to E\end{array} \right.\)