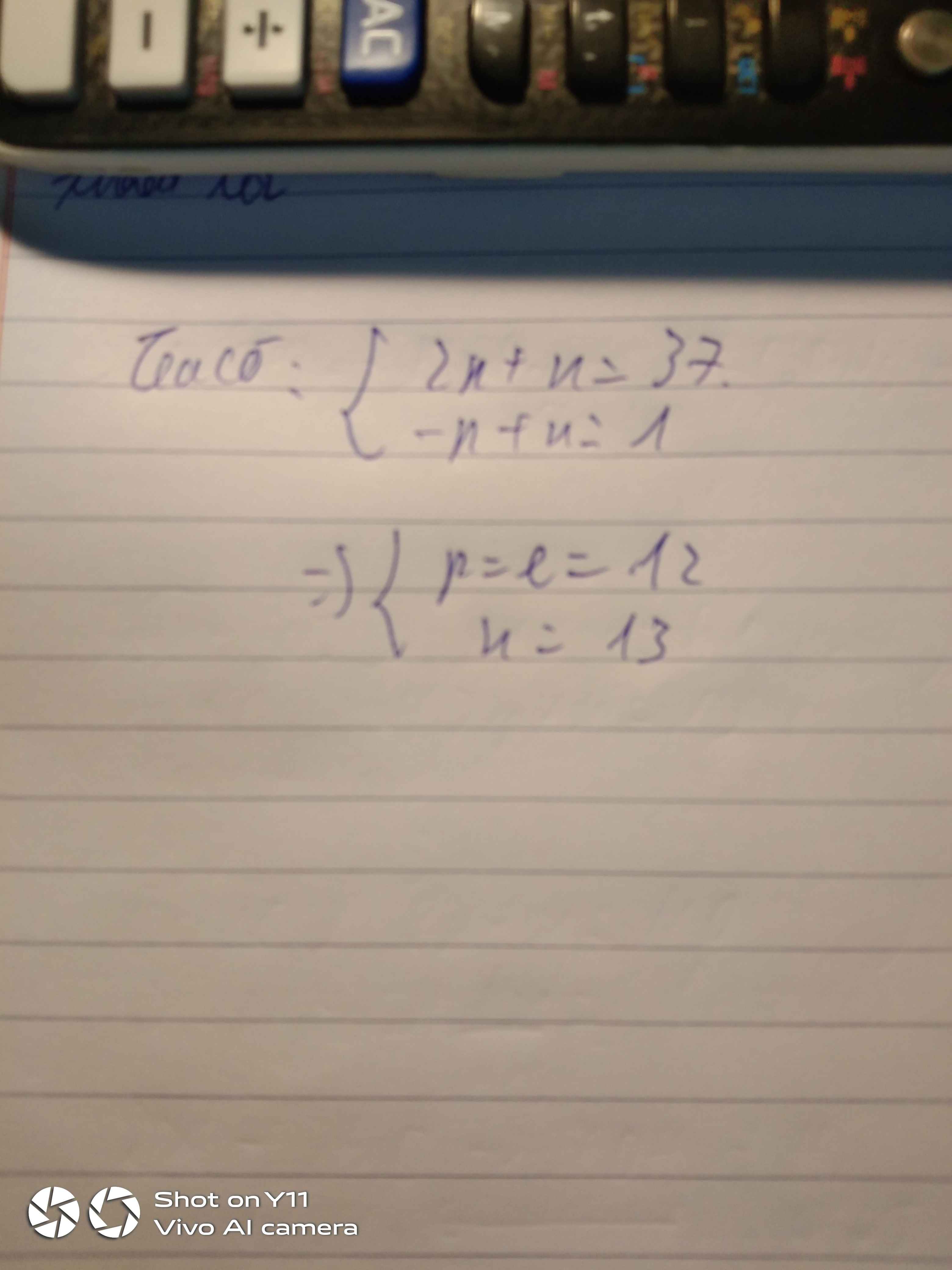Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số proton, notron, electron của nguyên tử nguyên tố X là px ; nx ; ex
Có : px = ex Mà px + ex + nx = 40 => 2px + nx = 40 (I)
Mặt khác : 2px - nx = 12 (II)
Từ (I) và (II) => px = ex = 13
nx = 14
=> số electron có trong nguyên tử nguyên tố X là 13

a) Theo đề bài ta có: \(p+n+e=34\) \(\Rightarrow2p+n=34\left(1\right)\)
Ta có: Số hạt mang điện nhiều hơn số hạt không mang điện là 10\(\Rightarrow p+e-n=10\Rightarrow2p-n=10\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}p=11\\n=12\end{matrix}\right.\)
\(\Rightarrow e=p=11\)
b) Nguyên tử khối của X: \(p+n=11+12=23\left(đvC\right)\)
Vậy X là Natri, kí hiệu là Na

gọi số hạt proton ,nơtron và electron của nt kim loại A là P1;N1 và E1
gọi số hạt proton ,nơtron và electron của nt kim loạiB là P2;N2;E2
Theo đb ta có :P1+N1+E1+P2+N2+E2=142 VÀ (P1+E1+P2+E2)-(N1+N2)=42
=> (P1+E1+P2+E2)=(142+42):2=92
Ta lại có:(P2+E2)-(P1+E1)=12
=>P2+E2=(92+12):2=52 VÌ SỐ P=E NÊN P2=E2=52/2=26
=>P1+E1=52-12=40 VÌ SỐ P=E NÊN P1=E1 =40/2=20
Sau đó tự kl nhé vs cả có j thì xem lại nha
p: hạt proton=electron
n: hạt notron
\(\begin{cases}2\left(p_A+p_B\right)+\left(n_A+n_B\right)=142\\2\left(p_A+p_B\right)-\left(n_A+n_B\right)=42\end{cases}\)
\(\Leftrightarrow\begin{cases}p_A+p_B=46\\n_A+n_B=50\end{cases}\)
Hạt mang điện của B nhiều hơn A:
\(\Leftrightarrow2\left(p_B-p_A\right)=12\Rightarrow p_B-p_A=6\)
Từ 3 phương trình trên:
\(\Rightarrow p_A=20\\ p_B=26\)

gọi só hạt proton, electron và notron lần lượt là p,e,n
ta có \(p=e\)
\(=>p+e=2p\)
Theo đề ta có:
\(\left\{{}\begin{matrix}2p+n=52\\n-p=1\end{matrix}\right.\)
\(=>p=17\) và \(n=18\)
=> số hạt proton, electron và notron lần lượt là 17,17,18

từ đề bài ta có:
1.p+n+e=116 mà số p= số e=)2p+n=116
2.hạt mạng điện là e và p=)2p-n=24
ta cộng cái trên cái dưới ra 4p=140=)p=35
từ đó suy ra số các hạt khác
Ta có: Tổng số proton, nơtron, electron là 116 ➩ e+p+n=116
Số hạt mang điện nhiều hơn số hạt không mang điện là 24 ➩ (e+p)-n=24
Vì e=p ➩\(\left\{{}\begin{matrix}\text{ e+p+n = (e+p)+n = 2p+n = 116 }\\(e+p)-n=2p-n=24\end{matrix}\right.\)
➩\(\left\{{}\begin{matrix}2p=\left(116+24\right):2\\n=\left(116-24\right):2\end{matrix}\right.\)
➩\(\left\{{}\begin{matrix}2p=70\\n=46\end{matrix}\right.\)
➩\(\left\{{}\begin{matrix}e=p=70:2=35\\n=46\end{matrix}\right.\)