Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

kết quả là 5 phút vì:
1 phút đầu thì rán 1 mặt của 4 cái đầu trước
phút thứ 2 thì ran 1 mặt cua 4 cai tiep theo
phut thu 3 thi ran thi ran 1 mat cua 2 cai cuoi va mat 2 cua 2 cai trong 4 cai dau
phut thu 4 thi ran 2 cai con lai trong 4 cai dau va 2 cai trong 4 cai tiep theo
phut thu 5 thi ran 2 cai trong 4 cai tiep theo va 2 cai cuoi



Giả sử hình vuông ABCD có tâm O và cạnh a, chứa năm hình tròn không cắt nhau và đều có bán kính bằng 1
Vì cả năm hình tròn này đều nằm trọn trong hình vuông nên các tâm của chúng nằm trong hình vuông \(A'B'C'D'\)có tâm O và cạnh \(a-2\), ở đây \(A'B'//AB\)
Các đường thẳng nối các trung điểm cùa các cạnh đối diện của hình vuông \(A'B'C'D'\)chia \(A'B'C'D'\)thành 4 hình vuông nhỏ
Theo nguyên lí Dirichlet tồn tại một trong 4 hình vuông nhỏ mà trong hình vuông này chứa ít nhất hai trong số 5 tâm hình tròn nói trên (không mất tính tổng quát ta giả sử là \(O'\)và \(O''\))
Để ý rằng vì không có hai hình tròn nào (trong số năm hình tròn) cắt nhau nên \(O'O''\ge2\)
Mặt khác do \(O'\)và\(O''\)cùng nằm trong một hình vuông nhỏ (cạnh của hình vuông nhỏ đó bằng \(\frac{a-2}{2}\)) nên ta lại có \(O'O''\le\frac{a-2}{2}.\sqrt{2}\). Từ đó ta suy ra được\(\frac{a-2}{2}.\sqrt{2}\ge2\Rightarrow a\ge2\sqrt{2}+2\)
Vậy mọi hình vuông cạnh a thỏa mãn yêu cầu đề bài, ta đều có \(a\ge2\sqrt{2}+2\)
Bây giờ xét hình vuông \(ABCD\)có \(a=2\sqrt{2}+2\)
Xét năm hình tròn có tâm là \(O,A',B',C',D'\)thì mọi yêu cầu của đề bài thỏa mãn.
Tóm lại, hình vuông có kích thước bé nhất cần tìm là hình vuông với cạnh \(a=2\sqrt{2}+2\)

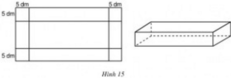
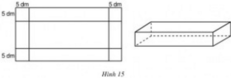
Gọi chiều rộng của miếng tôn là x(dm), x>10. Chiều dài của nó là 2x(dm).
Khi làm thành một cái thùng không đáy thì chiều dài của thùng là 2x-10(dm), chiều rộng là x-10 (dm), chiều cao laf5(dm).Dung tích của thùng là 5(2x-10)(x-10) d m 3
Theo đầu bài ta có phương trình:
5(2x-10)(x-10)=1500 hay x 2 - 15 x - 100 = 0
Giải phương trình: ∆ = 225 + 400 = 625 , ∆ = 25 ; x 1 = 20 , x 2 = - 5
Trả lời: Miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40(dm)

Diện tích 5 cái bánh hình tròn :
\(S_b=5.6.6.3,14.\dfrac{1}{4}=141,3\left(cm^2\right)\)
mà cái hộp đựng 5 cái bánh là hình vuông
Nên cạnh nhỏ nhất của cái hộp là : \(6.3=18\left(cm\right)\)