Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

THAM KHẢO:

Kẻ SM⊥BC
Mà BC⊥SO nên BC⊥(SOM). Suy ra BC⊥OM
Do đó góc nhị diện tạo bởi mặt bên và mặt đáy là \(\widehat{SMO}\)
Ta có: SO=98;OM=\(\dfrac{1}{2}\).180=90
tan \(\widehat{SMO}\)=\(\dfrac{SO}{OM}\)=1,1. Suy ra \(\widehat{SMO}\)=\(47,4^O\)
Vậy góc nhị diện tạo bởi mặt bên và mặt đáy là \(^{47,4^O}\)

tham khảo
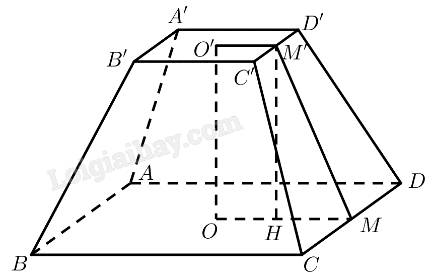
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy.Vậy \(AB=2a,A'B'=a,OO'=2a\)
a)Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'.\)
\(A'B'C'D'\) là hình vuông \(\Rightarrow O'M\perp C'D\)
\(CDD'C\) là hình thang cân \(\Rightarrow MM'\perp C'D'\)
Vậy \(\widehat{MM'O}\) là góc phẳng nhị diện giữa mặt bên và đáy nhỏ,\(\widehat{M'MO}\) là góc phẳng nhị diện giữa mặt bên và đáy lớn.
Kẻ \(M'H\perp OM\left(H\in OM\right)\)
\(OMM'O'\) là hình chữ nhật
\(\Rightarrow OH=O'M'=\dfrac{a}{2},OM=a,MH=OM-OH=\dfrac{a}{2}\tan\widehat{M'MO}=\dfrac{M'H}{MH}=4\)
\(\Rightarrow\widehat{M'MO}=75,96^o\Rightarrow\widehat{MM'O'}=180^o-\widehat{M'MO}\\ =104,04^o\)
b)Diện tích đáy lớn là:\(S=AB^2=4a^{^2}\)
Diện tích đáy bé là:\(S'=A'B'^2=a^2\)
Thể tích hình chóp cụt là:
\(V_1=\dfrac{1}{3}h\left(S+\sqrt{SS'}+S'\right)\\ =\dfrac{1}{3}.2a\left(4a^2+\sqrt{4a^2.a^2}+a^2\right)=\dfrac{14a^3}{3}\)
Thể tích hình trụ rỗng là:\(V_2=\pi R^2h=\pi\left(\dfrac{a}{2}\right)^2.2a=\dfrac{\pi a^3}{2}\)
Thể tích chân cột là:\(V=V_1-V_2=\left(\dfrac{14}{3}-\dfrac{\pi}{2}\right)a^3\)

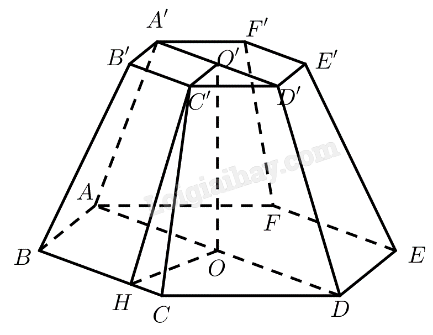
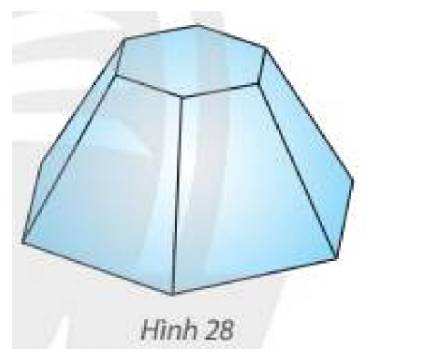
Mô hình hoá hình ảnh cái bục bằng hình chóp cụt lục giác đều \(ABC{\rm{DEF}}{\rm{.}}A'B'C'{\rm{D'E'F'}}\) có \(O\) và \(O'\) là tâm của hai đáy. Kẻ \(C'H \bot BC\left( {H \in BC} \right)\).
Ta có: \(BC = 1;CC' = B'C' = 0,7\).
Diện tích đáy lớn là: \(6.\frac{{B{C^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}\)
Diện tích đáy nhỏ là: \(6.\frac{{B'C{'^2}\sqrt 3 }}{4} = \frac{{147\sqrt 3 }}{{200}}\)
\(BCC'B'\) là hình thang cân nên \(HC = \frac{{BC - B'C'}}{2} = 0,15\)
Tam giác \(CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{\sqrt {187} }}{{20}}\)
Diện tích một mặt bên là: \(\frac{1}{2}\left( {BC + B'C'} \right).C'H = \frac{{17\sqrt {187} }}{{400}}\)
Diện tích sáu mặt bên là: \(6.\frac{{17\sqrt {187} }}{{400}} = \frac{{51\sqrt {187} }}{{200}}\)
Diện tích cần sơn là: \(\frac{{51\sqrt {187} }}{{200}} + \frac{{3\sqrt 3 }}{2} + \frac{{147\sqrt 3 }}{{200}} \approx 7,36\left( {{m^2}} \right)\)

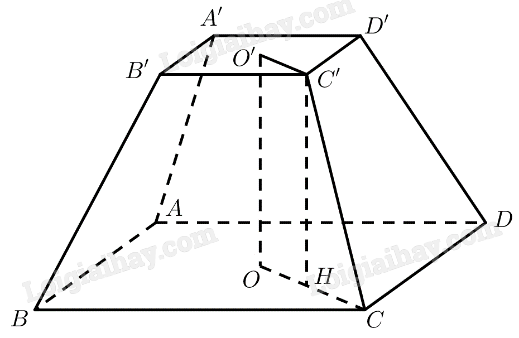
Mô hình hoá chân tháp bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 5,A'B' = 2,CC' = 3\).
\(ABCD\) là hình vuông
\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = 5\sqrt 2 \Rightarrow CO = \frac{1}{2}AC = \frac{{5\sqrt 2 }}{2}\)
\(A'B'C'D'\) là hình vuông \( \Rightarrow A'C' = \sqrt {A'B{'^2} + B'C{'^2}} = 2\sqrt 2 \Rightarrow C'O' = \frac{1}{2}A'C' = \sqrt 2 \)
Kẻ \(C'H \bot OC\left( {H \in OC} \right)\)
\(OHC'O'\) là hình chữ nhật \( \Rightarrow OH = O'C' = \sqrt 2 ,OO' = C'H \Rightarrow CH = OC - OH = \frac{{3\sqrt 2 }}{2}\)
\(\Delta CC'H\) vuông tại \(H \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \frac{{3\sqrt 2 }}{2} \Rightarrow OO' = C'H = \frac{{3\sqrt 2 }}{2}\)
Diện tích đáy lớn là: \(S = A{B^2} = {5^2} = 25\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = A'B{'^2} = {2^2} = 4\left( {{m^2}} \right)\)
Thể tích hình chóp cụt là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.\frac{{3\sqrt 2 }}{2}\left( {25 + \sqrt {25.4} + 4} \right) = \frac{{39\sqrt 2 }}{2}\left( {{m^3}} \right)\)
Số tiền để mua bê tông tươi làm chân tháp là: \(\frac{{39\sqrt 2 }}{2}.1470000 \approx 40538432\) (đồng).

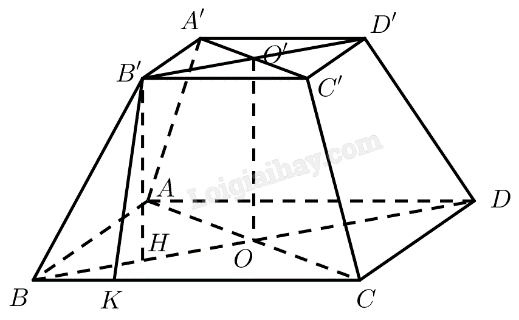
Gọi \(O\) và \(O'\) lần lượt là tâm của hai đáy.
Kẻ \(B'H \bot B{\rm{D}}\left( {H \in B{\rm{D}}} \right),B'K \bot BC\left( {K \in BC} \right)\)
\(\begin{array}{l}B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = 2a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = a\sqrt 2 \\B'D' = \sqrt {A'B{'^2} + A'{\rm{D}}{{\rm{'}}^2}} = a\sqrt 2 \Rightarrow B'O' = \frac{1}{2}B'{\rm{D'}} = \frac{{a\sqrt 2 }}{2}\end{array}\)
\(OO'B'H\) là hình chữ nhật \( \Rightarrow OH = B'O' = \frac{{a\sqrt 2 }}{2},B'H = OO' = a\)
\( \Rightarrow BH = BO - OH = \frac{{a\sqrt 2 }}{2}\)
Tam giác \(BB'H\) vuông tại \(H\) có: \(BB' = \sqrt {B'{H^2} + B{H^2}} = \frac{{a\sqrt 6 }}{2}\)
\(BCC'B'\) là hình thang cân \( \Rightarrow BK = \frac{{BC - B'C'}}{2} = \frac{a}{2}\)
Tam giác \(BB'K\) vuông tại \(K\) có: \(B'K = \sqrt {BB{'^2} - B{K^2}} = \frac{{a\sqrt 5 }}{2}\)

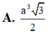
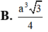
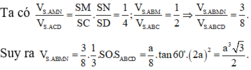
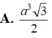
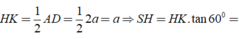
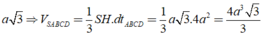
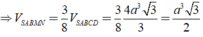
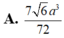
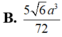
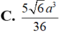
tham khảo:
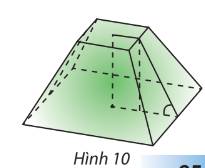
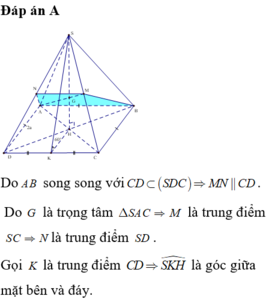
Mô hình hoá cái hầm bằng cụt chóp tứ giác đều \(ABCD.A'B'C'D'\) với \(O,O'\) là tâm của hai đáy. Vậy \(AB = 14,A'B' = 10\).
Gọi \(M,M'\) lần lượt là trung điểm của \(CD,C'D'\).
\(A'B'C'{\rm{D}}'\) là hình vuông \( \Rightarrow O'M' \bot C'{\rm{D}}'\)
\(CDD'C'\) là hình thang cân \( \Rightarrow MM' \bot C'D'\)
Vậy \(\widehat {MM'O'}\) là góc nhị diện giữa mặt bên và đáy nhỏ.
\( \Rightarrow \widehat {MM'O'} = {135^ \circ } \Rightarrow \widehat {M'MO} = {180^ \circ } - \widehat {MM'O'} = {45^ \circ }\)
Kẻ \(M'H \bot OM\left( {H \in OM} \right)\)
\(OMM'O'\) là hình chữ nhật
\( \Rightarrow OH = O'M' = 5,MH = OM - OH = 2,M'H = OO' = MH.\tan {45^ \circ } = 2\)
Diện tích đáy lớn là: \(S = A{B^2} = {14^2} = 196\left( {{m^2}} \right)\)
Diện tích đáy bé là: \(S' = A'B{'^2} = {10^2} = 100\left( {{m^2}} \right)\)
Số mét khối đất cần phải di chuyển ra khỏi hầm là:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right) = \frac{1}{3}.2\left( {196 + \sqrt {196.100} + 100} \right) = \frac{{872}}{3} \approx 290,67\left( {{m^3}} \right)\)