WO
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 4 2023
a. Gọi pt đường thẳng BC là: \(\Delta:y=ax+b\)
Vì pt đi qua 2 điểm B và C nên ta thay lần lượt các điểm vào, ta được:
\(\left\{{}\begin{matrix}-2=a.3+b\\-4=a.6+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+b=-2\\6a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{2}{3}\\0\end{matrix}\right.\)
Vậy pt đường thẳng BC là: \(y=-\dfrac{2}{3}x\)
b. \(d\left(A,\Delta\right)=\dfrac{\left|-\dfrac{2}{3}.\left(-1\right)+\left(-1\right).7\right|}{\sqrt{\left(-\dfrac{2}{3}\right)^2+\left(-1\right)^2}}=\dfrac{19\sqrt{13}}{13}\)
c. \(BC=\sqrt{\left(6-3\right)^2+\left(-4+2\right)^2}=\sqrt{13}\)
\(\Rightarrow S_{ABC}=\dfrac{\sqrt{13}.\dfrac{19\sqrt{13}}{13}}{2}=\dfrac{19}{2}\)
PT
1
CM
9 tháng 10 2017
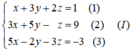
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và nhân phương trình (2) với 3 rồi trừ đi phương trình (3), phương trình (2) giữ nguyên ta được:
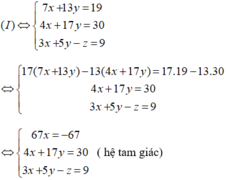
Giải hệ phương trình trên ta được x = -1; y = 2; z = -2.
Vậy hệ phương trình có nghiệm (x; y; z) = (-1; 2; -2)
WJ
1
SG
1
NT
0
Q
3
VN
26 tháng 6 2015
1. \(\sin^2x+\sin2x=3\cos^2x\Leftrightarrow\sin^2x+2\sin x\cos x-3\cos^2x=0\Leftrightarrow4\sin^2x+2\sin x\cos x-3=0\)
Vì \(\cos x=0\) không phải là nghiệm của phương trình, nên chia 2 vế pt cho \(\cos x\), ta đc:
\(4\tan^2x+2\tan x-\frac{3}{\cos^2x}=0\Leftrightarrow4\tan^2x+2\tan x-3\left(1+\tan^2x\right)=0\Leftrightarrow\tan^2x+2\tan x-3=0\)
Suy ra: \(\begin{matrix}\tan x=1\\\tan x=-3\end{matrix}\) suy ra x.
L
1 tháng 7 2015
b) \(\Leftrightarrow\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)=\sqrt{2}\sin2x\Leftrightarrow\sin\left(x+\frac{\pi}{4}\right)=\sin2x\Leftrightarrow\begin{cases}x+\frac{\pi}{4}=2x+k2\pi\\x+\frac{\pi}{4}=\pi-2x+k2\pi\end{cases}\)
\(\Leftrightarrow\begin{cases}x=\frac{\pi}{4}-k2\pi\\x=\frac{\pi}{4}+\frac{k2\pi}{3}\end{cases}\)
Vậy ....
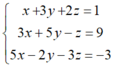
- Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện và sinα = a thì ta viết α = arcsin a.
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
- Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện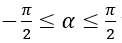
và sinα = a thì ta viết α = arcsin a.
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình cosx = a (2)
♦ |a| > 1: phương trình (2) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.
Khi đó phương trình (2) có các nghiệm là
x = α + k2π, k ∈ Z
và x = -α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện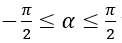
và cosα = a thì ta viết α = arccos a.
Khi đó các nghiệm của phương trình (2) là
x = arccosa + k2π, k ∈ Z
và x = -arccosa + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình tanx = a (3)
Điều kiện: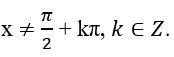
Nếu α thỏa mãn điều kiện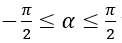
và tanα = a thì ta viết α = arctan a.
Khi đó các nghiệm của phương trình (3) là
x = arctana + kπ,k ∈ Z
- Phương trình cotx = a (4)
Điều kiện: x ≠ kπ, k ∈ Z.
Nếu α thỏa mãn điều kiện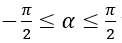
và cotα = a thì ta viết α = arccot a.
Khi đó các nghiệm của phương trình (4) là
x = arccota + kπ, k ∈ Z