Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7,2km/h = 2 m/s
72km/h = 20 m/s
Chọn chiều dương là chiều lên dốc, gốc tọa độ tại chân dốc, ta có :
Phương trình tọa độ của xe ô tô là:
x = 20.t + 0,4.t²/2 = 20t + 0,2t² (1)
Phương trình tọa độ của xe đạp là:
x' = 570 - 2.t - 0,2.t²/2 = 570 - 2t - 0,1t² (2) ( lấy v < 0 và a < 0 do nó có hướng ngược chiều dương )
Hai xe gặp nhau khi x = x'
=> 20t + 0,2t² = 570 - 2t - 0,1t²
<=> 0,3t² + 22t - 570 = 0
∆' = 11² - 0,3.(- 570) = 292
=> t = 20,3 (s)
=> x = 20.20,3 + 0,2.(20,3)² = 488,4 (m)
Vậy hai xe gặp nhau lúc t = 20,3 (s) và cách chân dốc x = 488,4 (m)
b)
Quãng đường ô tô đi được khi gặp nhau là:
s2 = x = 488,4 (m)
Vận tốc ô tô lúc đó là:
v2 = vo2 + at = 20 + 0,4.20,3 = 28,12 (m/s)
Quãng đường xe đạp đi được khi gặp nhau là:
s1 = 570 - 488,4 = 81,6 (m)
Vận tốc xe đạp lúc đó là:
v1 = vo1 + at = 2 + 0,2.20,3 = 6,06 (m/s)

Đổi \(21,6km/h=6m/s;43,2km/h=12m/s\)
Thời gian xuống dốc:
Ta có: \(v=v_0+at\Leftrightarrow t=\dfrac{v-v_0}{a}=\dfrac{12-6}{0,5}=12\left(m/s^2\right)\)
Chiều dài của dốc:
Ta có: \(s=v_0t+\dfrac{1}{2}at^2=6.12+\dfrac{1}{2}.0,5.12^2=108\left(m\right)\)

\(21,6\left(\dfrac{km}{h}\right)=6\left(\dfrac{m}{s}\right);4,2\left(\dfrac{km}{h}\right)=\dfrac{7}{6}\left(\dfrac{m}{s}\right)\)
\(a=\dfrac{v-v_0}{t}\Rightarrow t=\dfrac{v-v_0}{a}=\dfrac{6-\dfrac{7}{6}}{0,5}=\dfrac{29}{3}\left(s\right)\)
Ta có: \(v_0=21,6\)km/h=6m/s; \(v=4,2\)km/h=\(\dfrac{7}{6}\)m/s
Chọn chiều dương là chiều chuyển động.
Ta có:
\(v=v_0+at\Rightarrow t=\dfrac{v-v_0}{a}=\dfrac{\dfrac{7}{3}-6}{-0,5}=7,333s\)

\(36\left(\dfrac{km}{h}\right)=10\left(\dfrac{m}{s}\right)-54\left(\dfrac{km}{h}\right)=15\left(\dfrac{m}{s}\right)\)
\(t=\dfrac{v-v_0}{a}=\dfrac{15-10}{0,1}=50\left(s\right)\)
Ta có: \(v^2-v^2_0=2aS\)
\(=>S=\dfrac{v^2-v_0^2}{2a}=\dfrac{15^2-10^2}{2\cdot0,1}=625\left(m\right)\)
Vậy.............................
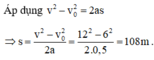
Đổi 54km/h=15m/s
Chiều dài của dốc là
\(s=\dfrac{v^2-v_0^2}{2a}=\dfrac{15^2-3^2}{2\cdot0,2}=540\left(m\right)\)
Thời gian xuống dốc :
\(t=\dfrac{v-v_0}{a}=\dfrac{15-3}{0,2}=60\left(s\right)\)