Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(F_k-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k-m.a}{mg}=...\)
b/ \(F_k.\cos30^0-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k.\cos30^0-m.a}{mg}\)

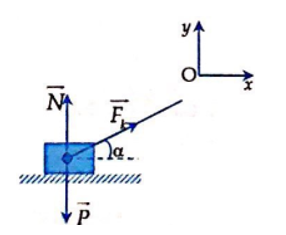
Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{F_k}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
Oy: \(N=P-Fsin\alpha\)
Ox: \(Fcos\alpha-\mu mg=m\cdot a\)
\(\Rightarrow a=\dfrac{Fcos\alpha-\mu mg}{m}=\dfrac{5cos30-0,2\cdot1\cdot10}{1}=2,33\)m/s2
Quãng đường vật sau 4s: \(S=\dfrac{1}{2}at^2=\dfrac{1}{2}\cdot2,33\cdot4^2=18,64m\)
Vận tốc sau 4s: \(v=a\cdot t=2,33\cdot4=9,32\)m/s
(sai bạn ạ)\(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{Fk}+\overrightarrow{Fms}=m\overrightarrow{a}\)\(\left(lấy-g=\dfrac{10m}{s^2}\right)\)
\(chiếuOy\Rightarrow N=P-F_k.sin30^o\)
\(chiếu-Ox\Rightarrow F_k.cos30^o-F_{ms}=ma\Rightarrow a^{ }=5.cos30^o-\mu\left(mg-F_k.sin30^o\right)=2,8m/s^2\)
\(\Rightarrow S=\dfrac{1}{2}at^2=22,4m\)
\(\Rightarrow v=\sqrt{2aS}=\sqrt{2.22,4.2,8}=11,2m/s\)
\(b,\)\(\Rightarrow a_{max}\Rightarrow a=\dfrac{F_k.cos\left(\alpha\right)-\mu\left(mg-F_k.sin\left(\alpha\right)\right)}{m}\)
\(a=5.cos\left(\alpha\right)-10\mu+\mu.5.sin\left(\alpha\right)=5\left[cos\left(\alpha\right)+\mu.sin\left(\alpha\right)\right]-2\)
\(\Rightarrow a_{max}\Leftrightarrow\left[cos\left(\alpha\right)+\mu.sin\left(\alpha\right)\right]_{max}\)
\(\Rightarrow\left[cos\left(\alpha\right)+\mu.sin\left(\alpha\right)\right]^2\le\left(1+\mu^2\right)\left[sin^2\left(\alpha\right)+cos^2\left(\alpha\right)\right]\le\left(1+0,2^2\right)=1,04\Rightarrow\left[cos\left(\alpha\right)+\mu sin\left(\alpha\right)\right]\le\sqrt{1,04}=1,01\Rightarrow a_{max}\Leftrightarrow\dfrac{1}{cos\left(\alpha\right)}=\dfrac{0,2}{sin\left(\alpha\right)}\Rightarrow\alpha=.....\)

Chọn A
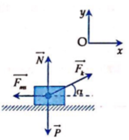
Vật chịu tác dụng của trọng lực P → , phản lực N → của mặt đường, lực kéo F K → và lực ma sát trượt . Chọn hệ trục Oxy như hình vẽ.
Áp dụng định luật II Niu-ton:
Chiếu lên trục Oy:
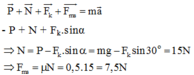
Chiếu lên trục Ox:
![]()
v = a.t = 0,58.5 = 2,9 m/s.

Áp dụng định luật II-Niuton ta có:
\(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}=m\overrightarrow{a}\)
Ta có: \(\left\{{}\begin{matrix}P=N+F.sin30\\F.cos30-F_{ms}=ma\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}N=P-Fsin30\\Fcos30-N\mu=ma\end{matrix}\right.\)
\(\Rightarrow F.cos30-\left(P-Fsin30\right)\mu=ma\)
\(\Leftrightarrow2.cos30-\left(1.10-2sin30\right)0,1=1.a\Rightarrow a=0,83\) m/s2

Chọn B.
Chọn Ox như hình vẽ
Áp dụng định luật II Niu-tơn ta được:

Công của lực kéo trong thời gian 5 giây kể từ khi bắt đầu chuyển động là:
A = Fscosα = 40,99.25.cos(30°) ≈ 887,5J

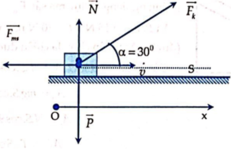
Chọn Ox như hình vẽ
Tính lực kéo theo định luật II Niu-tơn

Tính quãng đường đi dựa vào công thức chuyển động thẳng biến đổi đều:
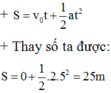
Công của lực kéo trong thời gian 5 giây kể từ khi bắt đầu chuyển động là
![]()

Theo định luật ll Niuton: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\)
Độ lớn lực kéo:
\(F=m.a+F_{ms}=m.a+\mu mg=50\cdot0,5+0,1\cdot50\cdot10=75N\)

a)Độ lớn lực ma sát:
\(F_{ms}=\mu mg=0,02\cdot10\cdot10=2N\)
Công lực ma sát: \(A_{ms}=F_{ms}\cdot s=2\cdot5=10m\)
b)Bảo toàn động năng:
\(A_F=\Delta W=\dfrac{1}{2}m\left(v_2^2-v_1^2\right)=\dfrac{1}{2}\cdot10\cdot\left(5^2-0^2\right)=125J\)
\(\Rightarrow F_k=\dfrac{A_F}{s}=\dfrac{125}{5}=25N\)