Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình 21.1G vẽ các lực tác dụng lên vật.
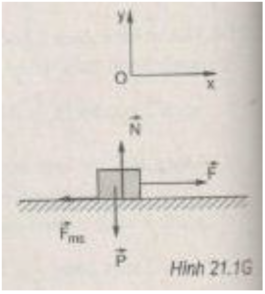
F = F m s = μ t mg = 0,30.1,0.9,8 = 2,94 N.

Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
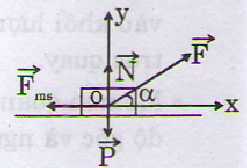
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2


Hình 21.1G vẽ các lực tác dụng lên vật.
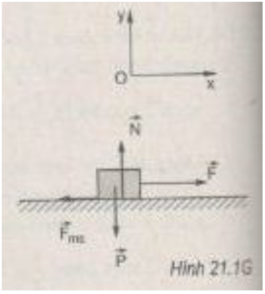
a = 2s/ t 2 = 2.0,8/4 = 0,40(m/ s 2 )
Áp dụng định luật II Niu-tơn ta có: P → + N → + F → + F m s → = m a → (1)
Chiếu (1) lên các trục tọa độ đã chọn ta được
Ox: F - μ t N = ma
Oy: N – mg = 0
Suy ra F = m(a + μ t g) = 1,0(0,40 + 0,30.9,8) = 3,34 N.

Gia tốc vật: \(S=\dfrac{1}{2}at^2\)\(\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot0,16}{4^2}=0,02\)m/s2
Định luật ll Niu-tơn:
\(F-F_{ms}=m\cdot a\)
\(\Rightarrow F=F_{ms}+m\cdot a=\mu mg+m\cdot a=0,2\cdot1\cdot10+1\cdot0,02=2,02N\)
Không có đáp án.

Gia tốc vật: \(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2S}{t^2}=\dfrac{2\cdot0,16}{4^2}=0,02\)m/s2
Lực ma sát: \(F_{ms}=\mu mg=0,2\cdot1\cdot10=2N\)
Định luật ll Niu-tơn:
\(F-F_{ms}=m\cdot a\)
\(\Rightarrow F_k=F_{ms}+m\cdot a=2+1\cdot0,02=2,02N\)

Chọn đáp án B
(vật chuyển động thẳng đều nên gia tốc a = 0)
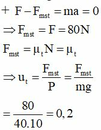

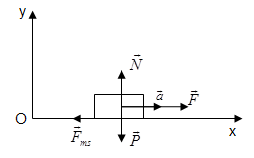
- Các lực tác dụng lên vật: Lực kéo \(\overrightarrow{F}\), lực ma sát\(\overrightarrow{F_{ms}}\), trọng lực \(\overrightarrow{P}\), phản lực \(\overrightarrow{N}\)
- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\left(1\right)\)
- Chiếu (1) lên trục Ox, Oy ta được:
\(\hept{\begin{cases}F-F_{ms}=m.a\\-P+N=0\end{cases}\Rightarrow\hept{\begin{cases}a=\frac{F-F_{ms}}{m}\\P=N\end{cases}}}\)
Có: \(F_{ms=\mu_t.N=\mu_t.P=\mu_t.mg}\)
→ Gia tốc chuyển động của vật: \(a=\frac{F-F_{ms}}{m}=\frac{F-\mu_t.mg}{m}\)

