Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=16t-0,5t^2\) \(\Rightarrow\) v0=16m/s; a=-1m/s2
Đây là chuyển động chậm dần đều.
a) Xét pt \(S=v_0.t+\dfrac{1}{2}a.t^2\) ta có:
\(v_0=16
\left(m\right);
a=-1
\) (m/\(s^2\))
=> Chuyển động chậm dần đều theo chiều dương TTĐ (vì a.v trái dấu)
b) Ta có: v = vo+at =16−t (m/s). Vật dừng lại khi v=0
<=> 16−t =0
<=> t =16
Vậy thời gian chuyển động của vật là t=16s

a) s=16t-0,5t2 ;(m/s)
\(\Rightarrow\)\(\left\{{}\begin{matrix}v_0=16\\a=-1\end{matrix}\right.\)
tính chất chuyển động :chuyển động chậm dần đều
b) x=x0+v0.t+a.t2.0,5=16t-0,5t2
O 16 15 14 v(m/s) t(s) 1 2

Chọn chiều dương là chiều chuyển động, gốc tọa độ trùng với vị trí ban đầu của vật, gốc thời gian là xuất phát.
a) Phương trình vận tốc: v = 6 + 4 t (m/s).
Đồ thị vận tốc - thời gian được biểu diễn như hình 12.
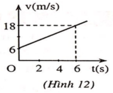
b) Khi v = 18 m/s thì t = 18 − 6 4 = 3 s.
Từ công thức v 2 − v 0 2 = 2 a s
quãng đường s = v 2 − v 0 2 2 a = 18 2 − 6 2 2.4 = 36 m.
c) Phương trình chuyển động: x = 6 t + 2 t 2 (m).
Khi v = 12 m/s thì t = 12 − 6 4 = 1 , 5 s ⇒ tọa độ x = 6.1 , 5 + 2.1 , 5 2 = 13 , 5 m.

\(v=v_0+at\)\(=-3t+6\)
\(\Rightarrow v_0=6m\)/s và \(a=-3m\)/s2
Phương trình chuyển động của vật:
\(x=x_0+v_0t+\dfrac{1}{2}at^2=6t+\dfrac{1}{2}\cdot\left(-3\right)\cdot t^2=6t-\dfrac{3}{2}t^2\)

a,Phương trình chuyển động của 1 vật
\(x=5+3t\left(m,s\right)\)
b,Vị trí của vật sau 4 s là:
\(x=5+3\cdot4=17\left(m\right)\)
c, <bạn tự vẽ ra nha>

