

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Công kéo: \(A_F=F\cdot s=40\cdot10=400J\)
Công của trọng lượng vật: \(A_P=P\cdot s=10m\cdot s=10\cdot3\cdot10=300J\)
Lực ma sát: \(F_{ms}=\mu mg=0,08\cdot3\cdot10=2,4N\)
Công của lực ma sát: \(A_{ms}=-F_{ms}\cdot s=-2,4\cdot10=-24J\)
b) Gia tốc vật: \(F-F_{ms}=m\cdot a\)
\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{40-2,4}{3}=\dfrac{188}{15}\left(m/s^2\right)\)
Vận tốc cần đạt: \(V=\sqrt{2aS}=\sqrt{2\cdot\dfrac{188}{15}\cdot10}\approx15,83m/s\)

a)\(v=54km/h=15m/s\)
Gia tốc của vật: \(v^2-v_0^2=2aS\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2S}=\dfrac{15^2-0^2}{2\cdot112,5}=1m/s^2\)
b)Theo định luật ll Niuton: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\Rightarrow F_{ms}=F-m.a=12-3\cdot1=9N\)
Hệ số ma sát: \(F_{ms}=\mu mg\)
\(\Rightarrow\mu=\dfrac{F_{ms}}{m\cdot g}=\dfrac{9}{3\cdot10}=0,3\)

Chọn A
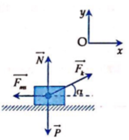
Vật chịu tác dụng của trọng lực P → , phản lực N → của mặt đường, lực kéo F K → và lực ma sát trượt . Chọn hệ trục Oxy như hình vẽ.
Áp dụng định luật II Niu-ton:
Chiếu lên trục Oy:
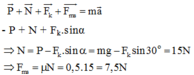
Chiếu lên trục Ox:
![]()
v = a.t = 0,58.5 = 2,9 m/s.

Áp dụng định luật II-Niuton ta có: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{F_{ms}}+\overrightarrow{N}=m\overrightarrow{a}\)
Chiếu vector lực theo phương ngang và phương thẳng đứng ta được
\(\left\{{}\begin{matrix}F-F_{ms}=ma\\P=N\end{matrix}\right.\)
\(\Rightarrow F-N\mu=ma\)
\(\Leftrightarrow F-mg\mu=ma\Leftrightarrow15-5.0,1.10=5a\Rightarrow a=2\) m/s2
Vận tốc của vật sau 3s là: \(v=v_0+at=0+2.3=6\) m/s
Một lò xo có khối lượng không đáng kể, một đầu được gắn cố định, đầu kia treo vật nặng có khối lượng m = 300 g, ở vị trí cân bằng lò xo dãn ra 6 cm. Lấy g = 10 m/s2
a. Tính độ cứng của lò xo.
b. Nếu treo thêm vật m’= 200 g vào đầu lò xo trên thì độ dãn của lò xo lúc ấy là bao nhiêu ?

Vật đang đứng yên\(\Rightarrow v_0=0\)m/s
Độ biến thiên động năng:
\(\Delta W=\dfrac{1}{2}m\left(v^2-v_0^2\right)=\dfrac{1}{2}\cdot1\cdot\left(20^2-0\right)=200J\)
Công cản: \(A_{ms}=\Delta W=200J\)
Lực cản: \(F_{cản}=\dfrac{A_{ms}}{s}=\dfrac{200}{100}=2N\)
Gia tốc vật: \(v^2-v^2_0=2aS\)
\(\Rightarrow a=\dfrac{v^2-v_0^2}{2S}=\dfrac{20^2-0}{2\cdot100}=2\)m/s2
Lực kéo F: \(F-F_{ms}=m\cdot a\)
\(\Rightarrow F=F_{ms}+m\cdot a=2+1\cdot2=4N\)

a) Dựng hệ trục tọa độ Oxy như hình vẽ. Chọn chiều (+) là chiều chuyển động của vật. Ta chiếu \(\overrightarrow{F_k}\) thành 2 lực \(\overrightarrow{F_{k_x}},\overrightarrow{F_{k_y}}\). Khi đó \(F_{k_x}=F_k.\cos60^o=24\left(N\right)\) và \(F_{k_y}=F_k.\sin60^o=24\sqrt{3}\left(N\right)\)
Áp dụng định luật II Newton, ta có: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_k}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}=5.\overrightarrow{a}\) (*)
Chiếu (*) lên Oy, ta được \(N=P-F_{k_y}=50-24\sqrt{3}\left(N\right)\)
Do đó \(F_{ms}=\mu.N=0,1\left(50-24\sqrt{3}\right)\approx0,843\left(N\right)\)
Chiếu (*) lên Ox, ta được:
\(F_{k_x}-F_{ms}=5.a\)
\(\Rightarrow48-0,843=5a\Leftrightarrow a=9,43\left(m/s^2\right)\)
b) Gọi \(v\) là giá trị vận tốc của vật sau khi vật đi được 16m. Do ban đầu vật đứng yên nên \(v_0=0\left(m/s\right)\). Ta có:
\(v^2-v_0^2=2as\Leftrightarrow v^2=2as=2.9,43.16=301,76\) \(\Rightarrow v\approx17,37\left(m/s\right)\)
c) Khi lực kéo dừng lại, thì chỉ còn lực ma sát trượt ảnh hưởng đến chuyển động của vật. Khi đó, gia tốc \(a'=\dfrac{-F_{ms}}{m}=-0,1686\left(m/s^2\right)\)
Như vậy, vật sẽ chuyển động chậm dần đều với gia tốc \(a'\approx-0,1686\left(m/s^2\right)\)

a)Độ lớn lực ma sát:
\(F_{ms}=\mu mg=0,02\cdot10\cdot10=2N\)
Công lực ma sát: \(A_{ms}=F_{ms}\cdot s=2\cdot5=10m\)
b)Bảo toàn động năng:
\(A_F=\Delta W=\dfrac{1}{2}m\left(v_2^2-v_1^2\right)=\dfrac{1}{2}\cdot10\cdot\left(5^2-0^2\right)=125J\)
\(\Rightarrow F_k=\dfrac{A_F}{s}=\dfrac{125}{5}=25N\)

Chọn đáp án D
Để vật chuyển động thẳng đều thì a = 0
Từ ( I ) ta có
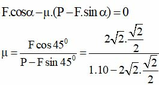
= 0,25