Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số sản phẩm sản xuất trong một ngày theo định mức.
Điều kiện x nguyên dương. Theo đề ta có chương trình:
\(\dfrac{360}{x}=\dfrac{360+\dfrac{360.5}{100}}{x+9}+1\)
⇔ x2 + 27x – 3240 = 0
⇒ x1= -72 (loại), x2 = 45.
Thời gian giao hoàn thành kế hoạch là = 8 ngày
Nếu sản xuất theo thời gian đã định với năng suất mới thì số sản phẩm làm được là (45+9).8=432 sản phẩm.

Gọi x (ngày) là số ngày dự định làm xong kế hoạch (x > 0).
Khi đó:
Số sản phẩm dự định làm trong một ngày là: 360/x (sản phẩm)
Thực tế, mỗi ngày làm thêm được 9 sản phẩm nên năng suất thực tế là: 360/x + 9 (sản phẩm / ngày)
Số ngày làm thực tế là: x – 1 (ngày)
Số sản phẩm làm được trong x – 1 ngày là: 360 + 360.5% = 378 sản phẩm.
Ta có phương trình:
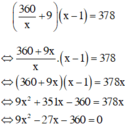
⇔ x = 8 (thỏa mãn) hoặc x = –5 (loại)
Số ngày dự định là 8 ngày, năng suất thực tế là 360:8 + 9 = 54 sản phẩm/ngày
Vậy khi đến hạn, phân xưởng sẽ làm được 54.8 = 432 sản phẩm.

Gọi 3 phân xưởng 1,2,3 sản xuất theo thứ tự là a,b,c
ta có \(a=\frac{1}{2}b=2c\) lại có \(a+b+c=630\) (1). Khi \(a=\frac{1}{2}b\Rightarrow b=2a\) (*) . Khi \(a=2c\Rightarrow c=\frac{a}{2}\) (**)
Thay (*) và (**) vào (1) ta có pt : \(a+2a+\frac{a}{2}=630\Leftrightarrow\frac{7}{2}a=630\Leftrightarrow a=180\)
Vậy a=180 ; b=360 ; c=90
Gọi số sản phẩm của phân xưởng 1 là a
số sản phẩm của phân xưởng 2 là b
số sản phẩm của phân xưởng 3 là c
Ta có:
\(a+b+c=630\)
\(2b+2c+c=630\)
\(4c+2c+c=630\)
\(7c=360\)
\(c=\frac{630}{7}\)
\(c=90\)
\(b=2c=2\times90=180\)
\(a=2b=2\times180=360\)
Vậy phân xưởng 1 sản xuất được 360 sản phẩm
phân xưởng 2 sản xuất được 180 sản phẩm
phân xưởng 3 sản xuất được 90 sản phẩm
Chúc bạn học tốt![]()

Gọi thời gian làm riêng của máy 1;2;3 lần lượt là a,b,c
Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b+c=95\\2c-a-b=10\\a=7b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{105}{2}\left(loại\right)\\b=\dfrac{15}{2}\left(loại\right)\\c=35\left(nhận\right)\end{matrix}\right.\)
=>Đề sai rồi bạn, số máy làm sao là số thập phân được

Gọi số sản phẩm mỗi ngày làm được theo dự định của 2 tổ là x (sản phẩm)
Và thời gian làm xong công việc theo dự định là y
Theo đề ra ta có
Tổ 1 làm thêm 4 sản phẩm 1 ngày so với dự định nên xong sớm 3 ngày thừa 58 sản phẩm ta có phương trình
(X+4)(y-3)-58=xy
Suy ra 4y-3x=70(*)
Tổ 2 làm thêm 3 sản phẩm nên xong sớm 3 ngày và thừa 54 sản phẩm ta có pt
(X+3)(y-2)-54=xy
Suy ra 3y-2x=60 (**)
Từ (*),(**) ta có hệ
4y-3x=70 và3y-2x=60
Giải hệ được y=40;x=30
Vậy số sản phẩm cần sản xuất theo dự định là xy=1200

Chọn C
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 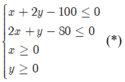
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0
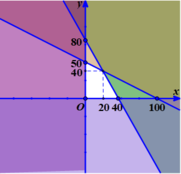
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.
+ Gọi x( x ≥ 0 ) là số kg loại I cần sản xuất,y ( y ≥ 0 ) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x+ 4y, thời gian là 30x+ 15y có mức lời là 40.000x+ 30.000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 120 giờ làm việc suy ra
2x+ 4y ≤ 200 hay x+ 2y- 100 ≤ 0 ; 30x+ 15y ≤ 1200 hay 2x+ y-80 ≤ 0
+ Tìm x; y thoả mãn hệ 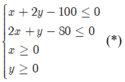
sao cho L( x; y) = 40.000x+ 30.000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng ( d) : x+ 2y-100= 0 và ( d’) : 2x+y-80=0

Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) =1.600.000;
L(0; 50) = 1.500.000; L(20; 40) = 2.000.000
suy ra giá trị lớn nhất của L(x; y) là 2.000.000 khi (x; y) =(20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.

Gọi x là số đơn vị sản phẩm loại I, y là số đơn vị sản phẩm loại II được nhà máy lập kế hoạch sản xuất. Khi đó số lãi nhà máy nhân được là P = 3x + 5y (nghìn đồng).
Các đại lượng x, y phải thỏa mãn các điều kiện sau:
(I)
(II)
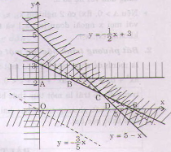
Miền nghiệm của hệ bất phương trình (II) là đa giác OABCD (kể cả biên).
Biểu thức F = 3x + 5y đạt giá trị lớn nhất khi (x; y) là tọa độ đỉnh C.
(Từ 3x + 5y = 0 => y = Các đường thẳng qua các đỉnh của OABCD và song song với đường y =
cát Oy tại điểm có tung độ lớn nhất là đường thẳng qua đỉnh C).
Phương trình hoành độ điểm C: 5 - x = <=> x = 4.
Suy ra tung độ điểm C là yc = 5 - 4 = 1. Tọa độ C(4; 1). Vậy trong các điều kiện cho phép của nhà máy, nếu sản xuất 4 đơn vị sản phẩm loại I và 1 đơn vị sản phẩm đơn vị loại II thì tổng số tiền lãi lớn nhất bằng:
Fc = 3.4 + 5.1 = 17 nghìn đồng.

Trong 11 ngày đầu làm được 11x112=1232(sp)
Trong 14 ngày sau làm được 14x125=1750(sp)
Cả tổ đã làm được 1232+1750=2982(sp)