Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
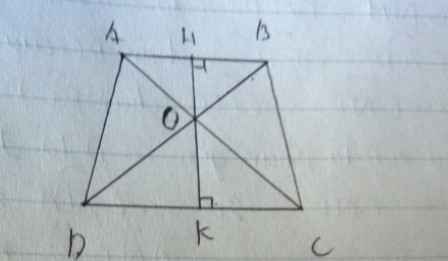
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
đề bài trên là đề bài sai đây mới là đề bài đúng :
Cho hình bình hành MNPQ có O là giao điểm của hai đường chéo và thỏa mãn MN = 8cm , NP = 5cm , OM = 3cm
Tính độ dài PQ , MQ , MP .
Giúp nhanh cho mình nha
a) Tính độ dài cạnh và độ dài hai đường chéo của hình thoi
a, Độ dài đường chéo ngắn: 3 x 2 = 6 (cm)
Độ dài đường chéo dài: 4 x 2 = 8 (cm)
Cạnh hình thoi: 5cm
b, Chu vi hình thoi: 5 x 4 = 20 (cm)
Diện tích hình thoi: (6 x 8) : 2 = 24 (cm2)
Đ.số:.....
Tham khảo:
- Vẽ đoạn thẳng AC =5 cm.
- Lấy A và C là tâm, vẽ hai đường tròn bán kính 3 cm (hình vẽ), hai đường tròn này cắt nhau tại hai điểm B và D.
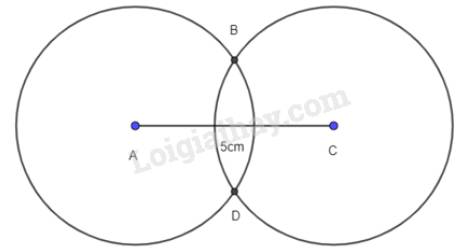
- Nối B với A, B với C, D với C.
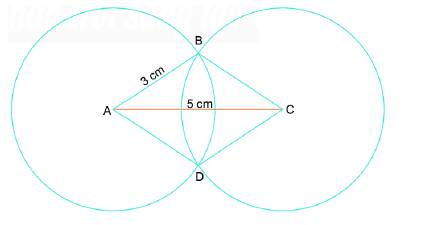
a) (hình tự vẽ)
Độ dài của đường chéo NQ là: \(2,4\cdot\dfrac{5}{8}=1,5\left(m^2\right)\)
Diện tích tấm bạt: \(\dfrac{1,5\cdot2,4}{2}\)= 1,8 (m2)
b) Độ dài của đoạn thẳng MO: 2,4 : 2=1,2(m)
___________________ AO: 1,2 : 2 =0,6 (m)
Diện tích của tam giác QAN: \(\dfrac{1,5\cdot0,6}{2}=0.45\left(m^2\right)\)
c) Đổi: 1,8 m2 = 180 dm2
Tấm bạt có giá: (180 : 5 ) * 3500 = 126000 (đồng)