Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai điểm M và N đối xứng nhau qua hệ trục Oxy.
Suy ra
\(\cos ( - \alpha )\)=\(\cos \alpha \); \(\sin ( - \alpha )\)= \( - \sin \alpha \)
b) Ta có:
\(\tan ( - \alpha )\) =\( - \tan \alpha \); \(\cot ( - \alpha )\)\( - \cot \alpha \)

Để đo góc giữa đường thẳng chứa tia sáng mặt trời và mặt phẳng nằm ngang tại một vị trí và một thời điểm cụ thể, ta cần sử dụng một thiết bị đo góc, thường được gọi là gnomon.
Cách thực hiện đo góc Mặt Trời như sau:
- Chọn một vị trí cố định trên mặt đất và đặt gnomon vào vị trí đó sao cho nó đứng thẳng đứng và vuông góc với mặt đất.
- Đợi cho đến khi đến thời điểm giữa trưa, khi tia sáng Mặt Trời đứng thẳng trên vị trí của bạn. Bạn có thể biết được thời điểm này thông qua các trang web hoặc ứng dụng dựa trên vị trí của bạn.
- Xác định bóng của gnomon trên mặt phẳng ngang và vẽ một đường thẳng từ đỉnh của gnomon đến đỉnh của bóng.
- Sử dụng thiết bị đo góc để đo góc giữa đường thẳng này và mặt phẳng ngang. Đó chính là góc Mặt Trời tại vị trí và thời điểm đó.

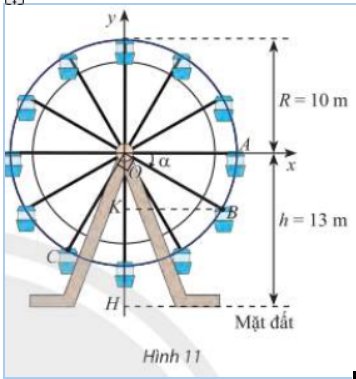
a) Điểm G là điểm biểu diễn cho góc lượng giác có số đo \(\alpha \). Khi đó tọa độ điểm \(G\left( {3cos\alpha ;{\rm{ }}3sin\alpha } \right)\).
Chiều cao của gàu ở vị trí G đến mặt nước là: \(3{\rm{ }} + {\rm{ }}3sin\alpha \) (m).
b) Khoảng cách của gàu đến mặt nước bằng 1,5m khi \(3 + 3sin\alpha = 1,5 \Leftrightarrow sin\alpha {\rm{ }} = \frac{{ - 1}}{2}\)
Một vòng quay là 30 giây và t nằm trong khoảng từ 0 đến 1 phút do đó t ∈ [0; 2π].

a) Hai thân cây cùng mọc vuông góc với mặt đất song song với nhau.
b) Mặt bàn và mặt đất song song với nhau.
c) Thanh xà ngang nằm trên trần nhà và mặt sàn nhà song song với nhau.

Khi một bàn thắng được ghi thì hình chiếu của quả bóng trên mặt đất theo phương thẳng đứng nằm phía trong vạch vôi cùng bờ với khung thành.

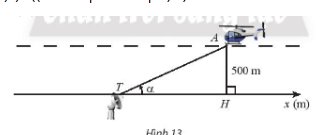
a, Xét tam giác AHT vuông tại H, ta có:
\(cot\alpha=\dfrac{TH}{AH}\Rightarrow TH=AH\cdot cot\alpha=500\cdot cot\alpha\)
Vậy trên trục \(T_x\) tọa độ \(x_H=500\cdot cot\alpha\)
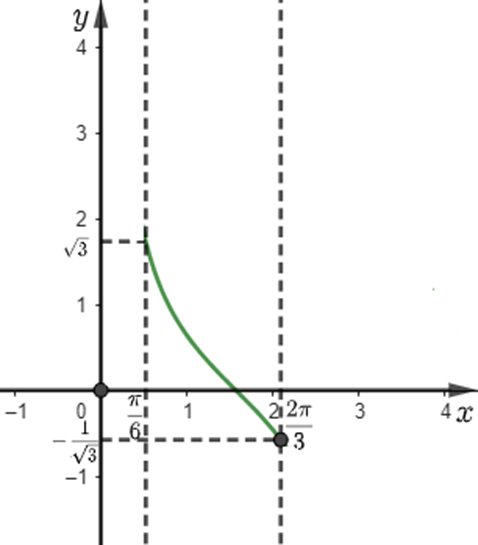
b, Ta có đồ thị của hàm số \(y=cot\alpha\) trong khoảng \(\dfrac{\pi}{6}< \alpha< \dfrac{2\pi}{3}\)
Khi đó:
\(-\dfrac{1}{\sqrt{3}}< cot\alpha< \dfrac{1}{\sqrt{3}}\Leftrightarrow-\dfrac{500}{\sqrt{3}}< 500\cdot cot\alpha< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-\dfrac{500}{\sqrt{3}}< x_H< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-288,7< x_H< 866\)
Vậy \(x\in\left\{-288,7;866\right\}\)

Các cột đèn được dựng thẳng đứng và vuông góc với mặt đường thì chúng song song với nhau. Do đó, đoạn thẳng nối hai chân cột chính là khoảng cách giữa hai đường thẳng song song.
Ta có thể nói khoảng cách giữa hai cột đèn đó là 5 m.

Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)
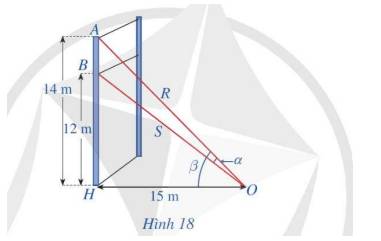



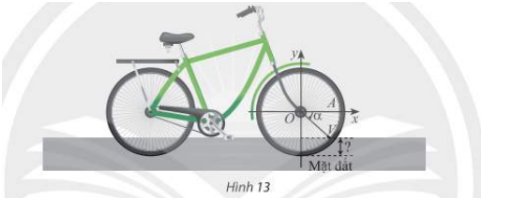
a) Ta có:
\(\begin{array}{l}\tan \widehat {AOB} = \frac{{AH}}{{HO}} = \frac{{14}}{{15}}\\\tan \beta = \frac{{BH}}{{HO}} = \frac{{12}}{{15}} = \frac{4}{5}\end{array}\)
Ta có: \(\tan \alpha = \tan \left( {\widehat {AOB} - \beta } \right) = \frac{{\tan \widehat {AOB} - \tan \beta }}{{1 + \tan \widehat {AOB.}\tan \beta }} = \frac{{\frac{{14}}{{15}} - \frac{4}{5}}}{{1 + \frac{{14}}{{15}}.\frac{4}{5}}} = \frac{{10}}{{131}}\)
b) \(\tan \alpha = \frac{{10}}{{131}} \Rightarrow \alpha \approx {4^o}\)