Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khi dây treo nghiêng góc α=300 so với phương thẳng đứng, vật M chịu tác dụng của các lựcnhư hình vẽ. Do gia tốc có phương ngang nên:\(T.\cos30^0=mg\) (1)
Mặt khác, xét theo phương hướng tâm MO ta có:
\(T-mg\cos30^0=\frac{mv^2}{l}\left(2\right)\) (Với v là vận tốc của vật tại M).
Từ (1) và (2) suy ra:\(v^2=\frac{gl}{2\sqrt{3}}\) (3)
Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí M và khi vật ở vị trí cân bằng ta được:
v02=v2+2gl(1 – cos300) = \(\frac{12-5\sqrt{3}}{6}gl\rightarrow\)v0 ≈ 2,36m/s
b) Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí \(\alpha\)=40o và khi vật ở vị trí cân bằng ta được:
\(v_0^2=v^2+2gl\left(l-\cos40^0\right)\rightarrow v=\sqrt{v_0^2-2gl\left(l-cos40^0\right)}\approx0,94\left(\frac{m}{s}\right)\)
Xét theo phương sợi dây ta có:
\(T=mgcos40^0+\frac{mv^2}{l}=0,1.10.cos40^0+\frac{0,1.0,94^2}{1}=0,86\left(N\right)\)

a) Chọn gốc thế năng trọng trường tại C ( Hình 92).
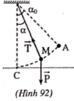
Theo định luật bảo toàn cơ năng: W A = W M
![]()
Vận tốc của m tại một điểm trên quỹ đạo ( ứng với góc lệch α )
![]()
Vận tốc v sẽ đạt cực đại khi cos α = 1 hay α = 0 .
![]()
b) Phương trình chuyển động của m: P → + T → = m a →
Chiếu phương trình lên phương bán kính đi qua M, chiều dương hướng vào điểm treo:
![]()
Thay ![]() vào phương trình của T ta được:
vào phương trình của T ta được:
Lực căng dây tại M ( ứng với góc lệch: T = m g 3 cos α - 2 cos α 0
Lực căng T đạt cực đại khi cos α = 1 hay α = 0 : T = m g 3 - 2 cos α 0

a) \(h=l-l\cos\alpha_0=1m\)
\(W=W_d+W_t=mgh=1J\)
b) Tính lực căng của dây treo khi vật qua vị trí cân bằng
Hai lực tác dụng vào vật: \(\overrightarrow{P},\overrightarrow{T}\)
Hợp lực: \(\overrightarrow{F}=\overrightarrow{P}+\overrightarrow{T}=m.\overrightarrow{a_{ht}}\)
\(m\frac{v^2_0}{l}=-P+T\)
\(T=m\frac{v^2_0}{l}+mg\)
\(T=3mg-2mg\cos\alpha_0=2N\)

Vận tốc: \(v=\sqrt{2gl(\cos\alpha-\cos\alpha_0)}\)
Lực căng dây: \(T=mg(3\cos\alpha-2\cos\alpha_0)\)
bạn có thể cho mình biết là tại sao v và lực căng dây lại được tính như vậy được ko ?

Đáp án B
- Chọn mốc thế năng là vị trí va chạm
- Xét thời điểm ngay khi va chạm mềm giữa viên đạn và bao cát là hệ kín
- Áp dụng định luật bảo toàn động lượng của hệ

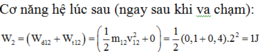
Sau khi cắm vào bao cát hệ chuyển động lên đến vị trí dây treo lệch với phương thẳng đứng một góc lớn nhất ![]() ứng với thế năng lớn nhất động năng bằng không vậy ta có:
ứng với thế năng lớn nhất động năng bằng không vậy ta có:
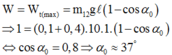

Đáp án B
- Chọn mốc thế năng là vị trí va chạm
- Xét thời điểm ngay khi va chạm mềm giữa viên đạn và bao cát là hệ kín
- Áp dụng định luật bảo toàn động lượng của hệ.
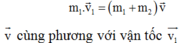
- Vận tốc của đạn và bao cát ngay sau va chạm là:
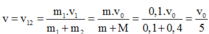
- Cơ năng hệ lúc sau (ngay sau khi va chạm):
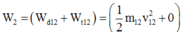

Sau khi cắm vào bao cát hệ chuyển động lên đến vị trí dây treo lệch với phương thẳng đứng một góc lớn nhất ứng với thế năng lớn nhất động năng bằng không vậy ta có:
![]()
![]()
- Bảo toàn cơ năng cho con lắc sau va chạm, ta được:
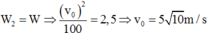


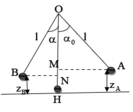
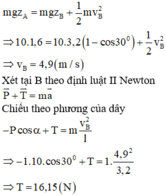
a, cơ năng tại các vị trí
cb \(W=\dfrac{1}{2}mv_0^2\)
30 độ \(W_{30}=mgl\left(1-cos30^o\right)\)
bảo toàn W
\(\Rightarrow v_0=\sqrt{2gl\left(1-cos30^o\right)}\approx1,637\left(m/s\right)\)
b,\(\alpha=40\)
\(v=\sqrt{2gl\left(1-cos40\right)}\approx2,16\left(m/s\right)\)
định luật II Niuton ta có
\(\overrightarrow{P}+\overrightarrow{T}=m.\overrightarrow{a}\) chiếu lên phương hướng tâm
\(T-P=m.a_{ht}\)
\(\Leftrightarrow T=P+m.\dfrac{v^2}{l}=mgcos40+m.\dfrac{v^2}{l}=...\)