Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P/s: Bạn tự vẽ hình minh họa để dễ hiểu hơn
Gọi \(\overrightarrow{p_1}\) là động lượng lúc trước và \(\overrightarrow{p_2}\) là động lượng lúc sau
Chọn (+) là chiều chuyển động ban đầu:
Từ mối liên hệ giữa động lượng và xung lượng của lực cho phần tử khí khi va chạm:
\(\overrightarrow{F}.\Delta t=\Delta\overrightarrow{p}\Leftrightarrow\overrightarrow{F}.\Delta t=\overrightarrow{p_2}-\overrightarrow{p_1}\)
chiếu (+) ta có: \(F.\Delta t=4.10^{-26}\left(-600-600\right)=-4,8.10^{-23}\left(N.s\right)\)

+ Theo bài ra ta có:
v 2 = v 1 = v = 600 m / s
+ Chọn chiều dương là chiều chuyển động của phần tử khí trước khi chạm vào thành bình ta có:
Δ p → = F → . Δ t
+ Chiếu theo chiều dương:
F . Δ t = − m . v 2 − m v 1 = − 2 m v
⇒ F . Δ t = − 2.4 , 65.10 − 26 .600 = − 5 , 58.10 − 23 N . s
Chọn đáp án A

Theo bài ra ta có: v2 = v1 = v = 600m/s
Chọn chiều dương là chiều chuyển động của phần tử khí trước khi chạm vào thành bình ta có Δ p → = F → . Δ t
Chiếu theo chiều dương:
F . Δ t = − m . v 2 − m v 1 = − 2 m v ⇒ F . Δ t = − 2.4 , 65.10 − 26 .600 = − 5 , 58.10 − 23 ( N . s )

Chon chiều dương như hình vẽ theo bài ra
v 1 = v 2 = v = 10 ( m / s )
Độ biến thiên động lượng
Δ p → = p → 2 − p → 1 = m v → 2 − m v → 1
Chiếu lên chiều dương
⇒ Δ p = − m v 2 sin α − m v 1 sin α = − 2 m v sin α
Lực trung bình do sàn tác dụng lên bóng
Δ p = F . Δ t ⇒ F = Δ p Δ t
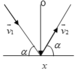
a. với α = 30 0
Ta có Δ p = − 2 m v sin α = − 2.0 , 5.10. sin 30 0 = − 5 ( k g m / s )
Lực trung bình do sàn tác dụng lên bóng
F = Δ p Δ t = − 5 0 , 1 = − 50 ( N )
b. Với α = 90 0
Ta có Δ p = − 2 m v sin α = − 2.0 , 5.10. sin 90 0 = − 10 ( k g m / s )
Lực trung bình do sàn tác dụng lên bóng
F = Δ p Δ t = − 10 0 , 1 = − 100 ( N )

Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)

Chọn chiều chuyển động ban đầu của quả cầu thứ nhất là chiều dương. Vì hệ vật gồm hai quả cầu chuyển động theo cùng phương ngang, nên tổng động lượng của hệ vật này có giá trị đại số bằng :
Trước va cham : p 0 = m 1 v 1 + m 2 v 2
Sau va chạm : p = m 1 v ' 1 + m 2 v ' 2
Áp dụng định luật bảo toàn động lượng, ta có :
p = p 0 ⇒ m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
Suy ra: v ' 2 = (( m 1 v 1 + m 2 v 2 ) - m 1 v ' 1 )/ m 2
Thay v ' 1 = - 0,6 m/s, ta tìm được
v ' 2 = ((2.3 + 3.1) - 2.0,6)/3 = 2,6(m/s)
Quả cầu thứ hai chuyển động với vận tốc 2,6 m/s theo hướng ban đầu.

a. Áp dụng định luật bảo toàn cơ năng xác định được vận tốc của hệ ngay sau khi va chạm là . Từ đó áp dụng định luật bảo toàn động lượng xác định được vận tốc của đạn (lúc đầu vận tốc của túi cát là 0), tức là
, từ đó suy ra v.
b. Áp dụng định luật bảo toàn năng lượng suy ra lượng năng lượng đã chuyển hóa thành nhiệt năng là bằng hiệu cơ năng của hệ lúc đầu và lúc sau, tức là

Ta có: \(\overrightarrow{F}\cdot\Delta t=\Delta\overrightarrow{p}=\overrightarrow{p_{sau}}-\overrightarrow{p_{trc}}\)
\(\Rightarrow F\cdot\Delta t=6,54\cdot10^{-26}\cdot\left(-244-244\right)=-3,19152\cdot10^{-23}N\cdot s\)