Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số cách xếp quanh bàn tròn là \(n\left(\Omega\right)=9!\)
Kí hiệu A là biến cố : "Nam nữ ngồi xen kẽ nhau"
Ta có :
\(n\left(A\right)=4!5!\) và \(P\left(A\right)=\dfrac{4!5!}{9!}\approx0,008\)

Không gian mẫu: \(8!\)
Có 2 kiểu xếp (kí hiệu N là nam, n là nữ): \(NnNnNnNn\) hoặc \(nNnNnNnN\)
Hoán vị 4 bạn nữ: \(4!\) cách
Hoán vị 4 bạn nam: \(4!\) cách
\(\Rightarrow2.4!.4!\) cách xếp thỏa mãn
Xác suất...

Số cách xếp 3 nam và 3 nữ vào 6 ghế là 6! Cách.
Suy ra: \(n\left(\Omega\right)=6!=720\)
a) Ta gọi A là biến cố : “Nam, nữ ngồi xen kẽ nhau”
Ta đánh số ghế như sau:
| 1 | 2 | 3 | 4 | 5 | 6 |
Trường hợp 1:
+ Nam ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nữ ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Trường hợp 2:
+ Nữ ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nam ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Suy ra:
N(A) = 3!.3! + 3!.3! = 36 + 36 = 72 cách xếp.
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{72}{720}=\dfrac{1}{10}=0,1\)
b) Gọi biến cố B: “Ba bạn nam ngồi cạnh nhau”
Xem 3 bạn nam như một phần tử N và N cùng 3 bạn nữ được xem như ngồi vào 4 ghế được đánh số như sau:
| 1 | 2 | 3 | 4 |
_ Số cách xếp N và 3 nữ vào 4 ghế là 4!
_ Mỗi cách hoán vị 3 nam cho nhau trong cùng một vị trí ta có thêm 3! cách xếp khác nhau.
Suy ra n(B) = 4!.3!=144
Vậy: \(P\left(B\right)=\dfrac{n\left(B\right)}{n\left(\Omega\right)}=\dfrac{144}{720}=\dfrac{1}{5}=0,2\)

Số cách xếp 3 nam và 3 nữ vào 6 ghế là 6! Cách.
Suy ra: n(Ω)=6!=720n(Ω)=6!=720
a) Ta gọi A là biến cố : “Nam, nữ ngồi xen kẽ nhau”
Ta đánh số ghế như sau:
|
1 |
2 |
3 |
4 |
5 |
6 |
Trường hợp 1:
+ Nam ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nữ ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Trường hợp 2:
+ Nữ ngồi ghế số 1, 3, 5 suy ra có 3! cách xếp
+ Nam ngồi ghế số 2, 4, 6 suy ra có 3! cách xếp
Suy ra trường hợp 1 có 3!.3! = 36 cách xếp
Suy ra:
N(A) = 3!.3! + 3!.3! = 36 + 36 = 72 cách xếp.
Vậy P(A)=n(A)n(Ω)=72720=110=0,1P(A)=n(A)n(Ω)=72720=110=0,1
b) Gọi biến cố B: “Ba bạn nam ngồi cạnh nhau”
Xem 3 bạn nam như một phần tử N và N cùng 3 bạn nữ được xem như ngồi vào 4 ghế được đánh số như sau:
|
1 |
2 |
3 |
4 |
_ Số cách xếp N và 3 nữ vào 4 ghế là 4!
_ Mỗi cách hoán vị 3 nam cho nhau trong cùng một vị trí ta có thêm 3! cách xếp khác nhau.
Suy ra n(B) = 4!.3!=144
Vậy : P(B)=n(B)n(Ω)=144720=15=0,2

Không gian mẫu là việc sắp xếp 6 bạn vào 6 ghế tùy ý
⇒ n(Ω) = P6 = 6! = 720.
a. Gọi A: “ Nam, nữ ngồi xen kẽ nhau”
+ Chọn chỗ ngồi cho 3 bạn nữ: Có 2 cách (Vị trí 1,3,5 hoặc 2,4,6).
+ Sắp xếp 3 bạn nữ vào 3 chỗ: Có 3! = 6 cách
+ Sắp xếp 3 bạn nam vào 3 chỗ còn lại: Có 3! = 6 cách
⇒ Theo quy tắc nhân: n(A) = 2.6.6 = 72 (cách).
⇒ n(A) = 2.3!.3! = 72
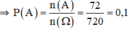
b. B: “Ban bạn nam ngồi cạnh nhau”
+ Chọn 3 chỗ ngồi cạnh nhau cho 3 bạn nam: Có 4 cách.
+ Sắp xếp 3 bạn nam vào 3 chỗ: Có 3! = 6 cách.
+ Sắp xếp 3 bạn nữ vào 3 chỗ còn lại: Có 3! = 6 cách
⇒ Theo quy tắc nhân: n(B) = 4.6.6 = 144 (cách)
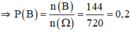
Xác suất để ba bạn nam ngồi cạnh nhau là:
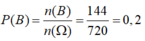

Chọn D
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
![]()

xếp ngẫu nhiên 8 bạn học sinh vào 4 bàn có 8! cách 40320 cách
=> \(n\left(\Omega\right)=40320\)
Gọi A:" có đúng 2 bàn mà trong đó mỗi bàn gồm 1 nam và 1 nữ "
=> \(n\left(A\right)=C^1_4.C^1_4..4.C^1_3.C^1_3.3.C^2_2.2.C^2_2.1=3456\) cách
=> P(A)= 3456/40320 =3/35

Đáp án B
Số phần tử KGM là: 9!. Mà số phần tử của biến cố các học sinh nữ luôn ngồi cạnh nhau là: 3!7!
Xác suất để các học sinh nữ luôn ngồi cạnh nhau là: 3 ! 7 ! 9 ! = 1 12

c. Trường hợp 1: bạn nam ngồi đầu. khi dó 2 bạn nam xếp vào 2 chỗ ( số ghế 1 và 3), nữ xếp nốt vào hai chỗ còn lại ( ghế số 2 và 4), số cách xếp là 2!.2!=4
Trường hợp 2: bnạ nữ ngồi đầu. Tương tự có 4 cách xếp . Vậy theo quy tắc cộng số phần tử của biến cố N là 4+4=8
Chọn C
1/35 bạn nhé!
Gọi A là biến cố "Các bạn nam và nữ ngồi xen kẻ nhau".
\(\left|\Omega\right|=7!\)
\(\left|\Omega_A\right|=3!.4!\)
\(\Rightarrow P\left(A\right)=\dfrac{3!.4!}{7!}=\dfrac{1}{35}\)