Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Lấy lần lượt 3 cuốn sách có 15.14.13 = 2730 cách
Lấy 2 cuốn sách đầu là Toán và cuốn còn lại là Văn có 10.9.5 = 450 cách
Xác suất để được hai cuốn sách đầu là Toán, cuốn thứ ba là Văn: ![]()

Đáp án B
Số cách chọn 3 cuốn sách trong 10 cuốn để phát ngẫu nhiên cho 3 bạn là A 10 3

Đáp án B.
Chọn 3 cuốn ngẫu nhiên từ 10 cuốn có C 10 3 cách.
Tặng 3 cuốn cho 3 bạn có 3! cách.
Suy ra số cách phát thưởng là 3!. C 10 3 = A 10 3 cách.

Có 5 cuốn sách Toán, 2 cuốn sách Lý và 1 cuốn sách Hóa đôi một khác nhau. Xếp ngẫu nhiên tám cuốn sách nằm ngang trên một cái kệ. Số cách xếp sao cho cuốn sách Hóa không nằm giữa liền kề hai cuốn sách Lý là:
A.39600
B. 720
C.30888
D. 38880
Nghĩa là loại đi trường hợp xếp mà có sự xuất hiện của bộ Lý-Hóa-Lý nằm đúng như vầy, sát nhau đồng thời Hóa kẹp giữa 2 Lý

Đáp án là A.
• Ta tìm số cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn.
Có 3 trường hợp :
• 7 cuốn còn lại gồm 2 môn toán lý : có C 9 7 cách
• 7 cuốn còn lại gồm 2 môn lý hóa : có C 11 7 cách
• 7 cuốn còn lại gồm 2 môn toán hóa : có C 10 7 cách
Suy ra có C 9 7 + C 11 7 + C 10 7 = 486 cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn. Do đó số cách chọn 8 cuốn sao cho 7 cuốn còn lại có đủ 3 môn là C 15 7 - 486 = 5949 cách.
Xác suất cần tìm là P = 5949 C 15 7 = 661 715

Đáp án B

Gọi biến cố A: “Số cuốn sách còn lại của thầy Tuấn có đủ cả ba môn”.
Khi đó ta có biến cố: A ¯ : “Số cuốn sách còn lại của thầy Tuấn không có đủ cả 3 môn”.


Chọn C
Xét phép thử T: “Chọn 7 cuốn sách từ 15 cuốn sách”.
Số phần tử của không gian mẫu trong phép thử là C 15 7 .
Gọi A biến cố chọn 7 cuốn sách có đủ 3 môn trong phép thử T.
Xác suất của biến cố cần tìm bằng xác suất của biến cố A.
Ta có ![]()
Vậy
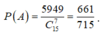
a) Gọi A là biến cố “Người mua sách A”; B là biến cố “Người mua sách B”; E là biến cố “Người đó không mua cả sách A và sách B”.
Khi đó \(\overline E \) là biến cố “Người đó mua sách A hoặc sách B”.
Ta có \(\overline E = A \cup B.\)
\(P\left( {\overline E } \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = 50\% + 70\% - 30\% = 90\% \)
Vậy xác suất để người mua đó mua ít nhất một trong hai sách A hoặc B là \(90\% \)
b) Ta có \(P\left( E \right) = 1 - P\left( {\overline E } \right) = 1 - 90\% = 10\% \)
Vậy xác suất để người mua đó không mua cả sách A và sách B là 10%.