Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\left\{{}\begin{matrix}p+e+n=58\\p=e\\p+e-n=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=40\\2p+n=58\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=19\\n=20\end{matrix}\right.\)

Đáp án:
K2O Giải chi tiết: Đặt số proton và notron của M lần lượt là p và n số proton và notron của X lần lượt là p' và n' Ta có hệ phương trình: ⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩2.(2p+n)+(2p′+n′)=140(1)(2.2p+2p′)−(2n+n′)=44(2)(p+n)−(p′+n′)=23(3)(2p+n)−(2p+n′)=34(4)Tu(1)va(2)⇒{2.(2p+p′)+(2n+n′)=1402.(2p+p′)−(2n+n′)=44⇒{2p+p′=46(5)2n+n′=48(6)Tu(3)va(4)⇒{(p−p′)+(n−n′)=232(p−p′)+(n−n′)=34⇒{p−p′=11(7)n−n′=12(8)Giai(5)va(7)⇒{p=19p′=8Giai(6)va(8)⇒{n=20n′=8{2.(2p+n)+(2p′+n′)=140(1)(2.2p+2p′)−(2n+n′)=44(2)(p+n)−(p′+n′)=23(3)(2p+n)−(2p+n′)=34(4)Tu(1)va(2)⇒{2.(2p+p′)+(2n+n′)=1402.(2p+p′)−(2n+n′)=44⇒{2p+p′=46(5)2n+n′=48(6)Tu(3)va(4)⇒{(p−p′)+(n−n′)=232(p−p′)+(n−n′)=34⇒{p−p′=11(7)n−n′=12(8)Giai(5)va(7)⇒{p=19p′=8Giai(6)va(8)⇒{n=20n′=8 Số khối của M là: A = p + n = 19 + 20 = 39 => M là Kali (kí hiệu: K) Số khối của X là: A' = p'+ n' = 8 + 8 = 16 => X là Oxi (kí hiệu: O) => CT hợp chất: K2O
Em tham khảo link này https://hoc24.vn/cau-hoi/cho-hop-chat-mx2-trong-phan-tu-nay-tong-so-hat-co-ban-la-140-va-so-hat-mang-dien-nhieu-hon-so-hat-ko-mang-dien-la-44-hatso-khoi-cua-x-lon-hon-so-kho.158928398419

Giả sử số hiệu nguyên tử, số nơtron trong nguyên tử của nguyên tố X lần lượt là Z, N.
Ta có hpt:
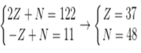
→ Nguyên tử X có số khối: A = Z + N = 37 + 48 = 85
→ Chọn C.

\(\left\{{}\begin{matrix}P+N+E=115\\P=E\\N-P=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2P+N=115\\N-P=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}P=E=35\\N=45\end{matrix}\right.\\ \Rightarrow A=P+N=35+45=80\left(đ.v.C\right)\)

Ta có: \(\left\{{}\begin{matrix}p+e+n=82\\p=e\\n-p=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3p=78\\p=e\\n=p+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}p=e=26\\n=30\end{matrix}\right.\)
\(\Rightarrow A=p+n=26+30=56\left(u\right)\)