Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi AB là chiều cao của ngọn hải đăng (A là chân của ngọn hải đăng), AC là độ dài bóng của ngọn hải đăng trên mặt đất và \(\widehat{C}\)là góc hợp bởi tia nắng mặt trời với mặt đất.
Khi đó \(\Delta ABC\)vuông tại A \(\Rightarrow AB=AC.\tan C=20.\tan35^o\approx14\left(m\right)\)(đáp án ra \(14,00415076...\)mà đề yêu cầu làm tròn đến chữ số thập phân thứ nhất tức đáp án sẽ là \(14,0\)hay \(14\))
Vậy chiều cao của ngọn hải đăng là khoảng \(14m\)

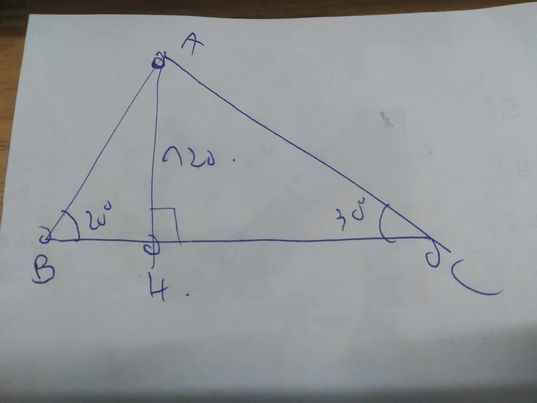
Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát

chiếc thuyền đang đúng cách chân hải đăng \(\approx\)63,40m![]()
Trong \(\Delta\)ABC cóA= \(\overset{ }{ }\)900 (gt)
\(\tan\)C=\(\dfrac{AB}{AC}\) (Định nghĩa tỉ số lượng giác)
T/s:\(\tan\) 270 =\(\dfrac{AB}{300}\)
\(\Rightarrow\) AB=\(\tan\)270 *300
\(\approx\) 152,85 m
bạn lấy tan 270 *300m là ra kết quả này, nó chỉ ra xấp xỉ thôi bn