Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)

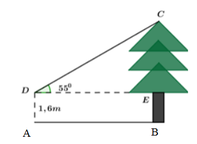
Đặt các điểm D, E như hình vẽ.
Xét CDE vuông tại E ta có:
![]()
Chiều cao của cây là BC = CE + BE = 8,57 + 1,6 = 10,17m
Đáp án cần chọn là: D

Đáp án:
Giải thích các bước giải:
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD – CK = CD – EF = 2 – 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9

A B C E F
Gọi C là điểm đặt mắt người đó, BE là chiều cao của cây và CF là chiều cao người đó
Xét tứ giác AECF có:
\(\widehat{A}=\widehat{E}=\widehat{F}=90^0\)
=> AECF là hình chữ nhật
=> \(AE=CF=1,7m;AC=EF=30m\)
Áp dụng tslg trong tam giác ABC:
\(tanC=\dfrac{AB}{AC}\Rightarrow AB=30.tan35^0\approx21\left(m\right)\)
Chiều cao của cây: \(BE=AB+AE\approx21+1,7\approx23\left(m\right)\)
Lời giải:
Theo hình vẽ ta có:
$BC=DE=1,7$ (m)
$AB=BE.\tan \widehat{AEB}=30.\tan 35^0=21$ (m)
Chiều cao của cây là:
$AC=AB+BC=21+1,7=22,7$ (m)

Chiều cao của cái cây đó là:
4,5*tan55\(\simeq6,43\left(m\right)\)
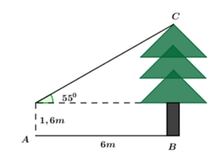

Với góc nhìn tạo với phương nằm ngang là 42 độ, ta có:
tan(42°) = h / 15
Để tìm giá trị của h, ta cần giải phương trình trên để tìm giá trị của h.
tan(42°) = h / 15
h = tan(42°) * 15
Sử dụng máy tính, ta tính được:
h ≈ 15.7m
Vậy, chiều cao của cây là khoảng 15.7m.
idol k11 đây chăng =)?