Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 4 giờ 20 phút= 13/3 giờ
Gọi độ dài quãng đường AC là x(km)
Gọi độ dài quãng đường CB là y(km)
Điều kiện x > 0 và y > 20
Lúc đó thời gian người đi xe máy đi trên quãng đường AC là x/30 (giờ)
Thời gian người đi xe máy đi trên quãng đường CB là y/20 (giờ)
Theo đề bài, thời gian cả thảy đi từ A đến B là 4 giờ 20 phút nên ta có phương trình:
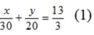
Vì quãng đường AB ngắn hơn quãng đường BC là 20 km nên ta có phương trình: y – x = 20 (2)
Từ (1) và (2) ta có hệ phương trình:


Vậy quãng đường AC dài 40km, quãng đường CB dài 60km.

Lời giải:
Đổi 4h30 = $4,5$ h
Vận tốc trên quãng đường CB là $a$ km/h thì vận tốc trên $AC$ là $a+20$ (km/h)
Quãng đường $AC=BC+10$ (km)
Tổng thời gian đi quãng đường AB: $\frac{AC}{v_{AC}}+\frac{CB}{v_{CB}}=4,5$
$\Leftrightarrow \frac{BC+10}{a+20}+\frac{BC}{a}=4,5$
Khai thác được đến đây thì không biết bạn muốn tìm cái gì?

Lời giải:
Đổi $4h30'=4,5$h
Thời gian đi quãng đường $AC$: $\frac{AC}{30}$ (h)
Thời gian đi quãng đường $CB$: $\frac{CB}{20}=\frac{AC-10}{20}$ (h)
Ta có:
$\frac{AC}{30}+\frac{AC-10}{20}=4,5$$\Leftrightarrow \frac{AC}{12}=5\Rightarrow AC=60$ (km)
$CB=60-10=50$ (km)
Lời giải:
Đổi $4h30'=4,5$h
Thời gian đi quãng đường $AC$: $\frac{AC}{30}$ (h)
Thời gian đi quãng đường $CB$: $\frac{CB}{20}=\frac{AC-10}{20}$ (h)
Ta có:
$\frac{AC}{30}+\frac{AC-10}{20}=4,5$$\Leftrightarrow \frac{AC}{12}=5\Rightarrow AC=60$ (km)
$CB=60-10=50$ (km)

Gọi độ dài quãng đường AC là x
=>Độ dài CB là x+20
Theo đề, ta có: x/30+(x+20)/20=4+1/3=13/3
=>x/30+x/20=13/3-1=10/3
=>x=40
=>CB=60km