Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi quãng đường AB là x.ĐK: x>0
khi đó thời gian mà người đi xe đạp với vận tốc 12 (km/h) là x/12 (h)
thời gian mà người đó khi về với vận tốc 15 km/h là (x+2,5)/15
đổi 20'=1/3 h
theo bài ra ta có phương trình:
x/12 + (x+2.5)/15=1/3
=>5x+4(x+2,5)=20
<=> 5x+4x+10=20
<=>x=10/9(TM)
Vậy quãng đường AB là 10/9 km

Gọi chiều dài con đường lúc đi là x ( km, x > 0 )
Gọi chiều dài quãng đường lúc về là x + 15 ( km )
Thời gian đi quãng đường lúc đầu là: \(\frac{x+15}{20}\left(h\right)\)
Ta có phương trình:
\(\frac{x}{15}+\frac{x+15}{20}=9,5\)
\(\Leftrightarrow\frac{4x}{60}+\frac{3x+45}{60}=\frac{570}{60}\)
\(\Leftrightarrow4x+3x+45=570\)
\(\Leftrightarrow4x+3x+45-570=0\)
\(\Leftrightarrow7x-525=0\)
\(\Leftrightarrow7x=525\)
\(\Leftrightarrow x=525:7=75\)( thỏa mãn )
Vậy chiều dài quãng đường lúc đi là 75 km
\(\)

Gọi Quãng đường AB là x ( x > 0, km )
Quãng đường khi về là x + 10 km
Thời gian người đó đi quãng đường AB là \(\frac{x}{25}\)giờ
Thời gian người đó đi quãng đường khi về là \(\frac{x+10}{30}\)giờ
Do thời gian về ít hơn thời gian đi là 20 phút = 1/3 giờ
nên ta có phương trình \(\frac{x}{25}-\frac{x+10}{30}=\frac{1}{3}\Leftrightarrow x=100\)
Vậy Quãng đường AB là 100 km

Đặt AB=x
=>BC=x+24
Theo đề, ta có: \(\dfrac{x}{4}+\dfrac{x+24}{40}=\dfrac{2x+24}{16}\)
=>1/4x+1/40x+3/5=1/8x+3/2
=>x=6
=>AC=2*6+24=36km
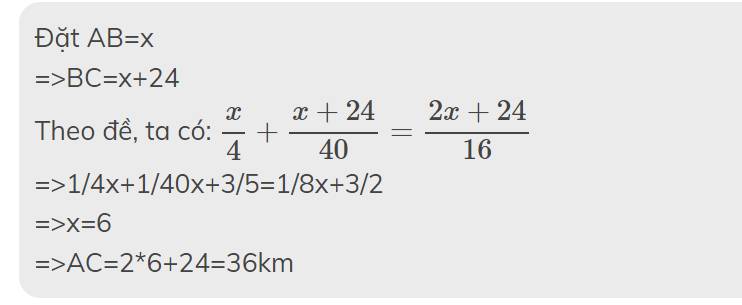
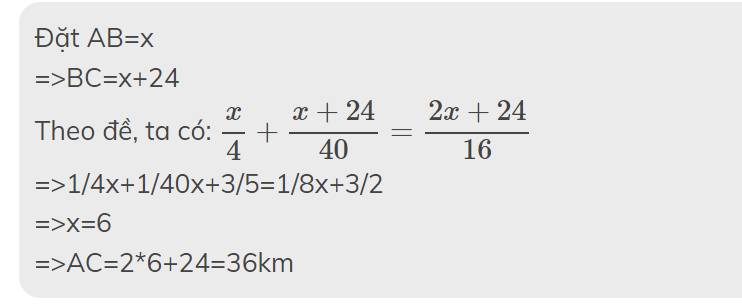
Gọi độ dài quãng đường đi là x (km) với x>0
Thời gian đi là: \(\dfrac{x}{12}\) giờ
Độ dài quãng đường về là: \(x+4\) (km)
Thời gian về là: \(\dfrac{x+4}{20}\) giờ
Do tổng thời gian cả đi và về là 6h nên ta có pt:
\(\dfrac{x}{12}+\dfrac{x+4}{20}=6\)
\(\Leftrightarrow\dfrac{x}{12}+\dfrac{x}{20}=6-\dfrac{4}{20}\)
\(\Leftrightarrow\dfrac{2}{15}x=\dfrac{29}{5}\)
\(\Rightarrow x=43,5\left(km\right)\)