Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn chiều dương là chiều chuyển động.
Trong quá trình chuyển động, tủ lạnh chịu tác dụng của 4 lực: Trọng lực P, phản lực N, lực ma sát Fms, lực đẩy Fd.
Áp dụng định luật II Newton, ta có:
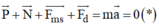
(chuyển động đều nên a = 0)
Chiếu (∗) lên phương chuyển động ta có:
-Fms + Fd = 0 ⇔ Fd = Fms = μN = 0,51. 890 = 453,9N
(Lưu ý vì trọng lực , phản lực cân bằng nhau theo phương thẳng đứng nên N = P = 890 (N)).
Với giá trị của lực đẩy này, ta không thể làm tủ lạnh chuyển động được từ trạng thái nghỉ vì hợp lực tác dụng lên vật bị triệt tiêu (bằng 0) vật đứng yên sẽ tiếp tục đứng yên.
Với giá trị của lực đẩy này, ta không thể làm tủ lạnh chuyển động được từ trạng thái nghỉ vì hợp lực tác dụng lên vật bị triết tiêu ( bằng 0) vật đứng yên sẽ tiếp tục đứng yên.

Ta có phương trình chuyển động của vật
(do tủ chuyển động thẳng đều)
Chọn chiều dương là chiều chuyển động.
=> Fđ – Fms = 0
=> Fđ = Fms = μN (N = P)
=> Fđ = μP = 0,51 x 890
=> Fđ = 453,9N
+ Với lực đẩy tìm được không thể làm cho tủ lạnh chuyển động từ trạng thái nghỉ vì lực được vì lực làm cho tủ lạnh chuyển động từ đứng yên lớn hơn lực giữ cho tủ lạnh chuyển động thẳng đều.
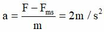
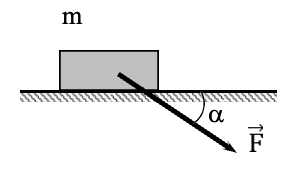
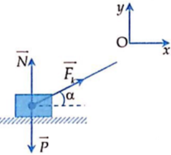
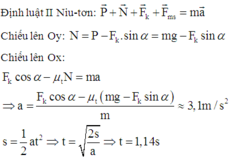
a. Độ lớn lực đẩy theo phương ngang: \(F_x=F.cos45^0=80.cos45^0=40\sqrt{2}\left(N\right)\)
Độ lớn lực đẩy theo phương thẳng đứng: \(F_y=F.sin45^0=80.sin45^0=40\sqrt{2}\left(N\right)\)
b. Gia tốc chuyển động: \(a=\dfrac{v}{t}=\dfrac{1,2}{3}=0,4\left(\dfrac{m}{s^2}\right)\)
Áp dụng định luật II Newton có: \(\overrightarrow{F}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m\overrightarrow{a}\) (*)
Chiếu (*) lên phương Ox, chiều dương trùng với chiều chuyển động:
\(F_x-F_{ms}=ma\)
\(\Leftrightarrow40\sqrt{2}-F_{ms}=15.0,4\)
\(\Rightarrow F_{ms}=40\sqrt{2}-6\left(N\right)\)