Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực ma sát tác dụng vào thùng là:
→ F m s = μ N = μ m g = 0 , 35.50.10 = 175 N
Nhận thấy Lực ma sát tác dụng vào thùng lớn hơn lực đẩy của người đẩy thùng nên thùng không chuyển động.
Đáp án: C

Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\) (1)
Lực ma sát: \(F_{ms}=\mu mg=0,02\cdot80\cdot10=16N\)
Thay vào (1) ta đc:
\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{150-16}{80}=1,675\)m/s2
Chọn B.

Chọn hệ trục tọa độ Oxy như hình vẽ. Gọi \(\overrightarrow{F_k}\) là lực kéo tác dụng lên sợi dây, \(\overrightarrow{P}\) và \(\overrightarrow{N}\) lần lượt là trọng lực tác dụng lên vật. Ta phân tích \(\overrightarrow{F_k}\) thành 2 lực \(\overrightarrow{F_{k_x}}\) và \(\overrightarrow{F_{k_y}}\) trên các trục Ox, Oy.
a) Công của lực kéo là \(A_k=F_k.s.cos\left(\overrightarrow{F_k},\overrightarrow{s}\right)=100.20.cos45^o=1000\sqrt{2}\left(J\right)\)
b) Gọi \(\overrightarrow{F_{ms}}\) là lực ma sát tác dụng lên vật. Chọn chiều dương là chiều chuyển động của vật
Áp dụng định luật II Newton:
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\) (1)
Chiếu (1) lên Oy: \(N=P-F_{k_y}=400-F_k.sin45^o=400-175\sqrt{2}\left(N\right)\)
Do đề bài không nói gì về loại chuyển động của vật nên mình sẽ xem đây là chuyển động nhanh dần đều nhé. Khi đó, ta sẽ có \(s=\dfrac{1}{2}at^2\Rightarrow20=\dfrac{1}{2}a.180^2\) \(\Rightarrow a=\dfrac{1}{810}\left(m/s^2\right)\).
Chiếu (1) lên Ox, ta được \(F_{k_x}-F_{ms}=m.a\Rightarrow F_{ms}=F_{k_x}-m.a=350.cos45^o-400.\dfrac{1}{180}\)\(=170\sqrt{2}-\dfrac{20}{9}\) (N)
\(\Rightarrow A_{ms}=-\left(170\sqrt{2}-\dfrac{20}{9}\right).20\approx-4763,88\left(J\right)\)

Định luật ll Niu tơn: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\)
\(\Rightarrow F-\mu mg=m.a\)
Gia tốc thùng:
\(\Rightarrow a=\dfrac{F-\mu mg}{m}=\dfrac{180-0,25\cdot50\cdot9,8}{50}=1,15\left(m/s^2\right)\)

a) Do vật di chuyển theo phương ngang nên \(N=P=mg=50.10=500\left(N\right)\)
Ta có \(F_{ms}=\mu N=0,4.500=200\left(N\right)\)
b) Áp dụng định luật II Newton, ta có \(\overrightarrow{F}=m\overrightarrow{a}\)
Chiếu lên phương chuyển động của vật, ta có
\(F_k-F_{ms}=ma\) \(\Leftrightarrow a=\dfrac{F_k-F_{ms}}{m}=\dfrac{220-200}{50}=0,4\left(m/s^2\right)\)
c) Quãng đường thùng dịch chuyển: \(s=\dfrac{1}{2}at^2=\dfrac{1}{2}.0,4.10^2=20\left(m\right)\)
d) Vận tốc của vật sau khi di chuyển được 2 giây: \(v=at=0,4.2=0,8\left(m/s\right)\)
a)
Độ lớn lực ma sát trượt giữa thùng và mặt sàn:
\(F_{mst}=\mu.N=0,4.50.10=200\left(N\right)\)
b)
Gia tốc của thùng: \(a=\dfrac{F}{m}=\dfrac{F_{kéo}-F_{ms}}{m}=\dfrac{220-200}{50}=0,4\left(m/s^2\right)\)
(Chiếu theo chiều chuyển động)
c)
Sau 10s kể từ khi bắt đầu di chuyển, thùng trượt được quãng đường:
\(s_{10}=\dfrac{1}{2}.0,4.10^2=20\left(m\right)\)
d)
Vận tốc của thùng sau khi di chuyển được 2s:
\(v=at=0,4.2=0,8\left(m/s\right)\)

a) Muốn cho vật dịch chuyển thì phải đẩy nó với một lực theo phương nằm ngang có độ lớn lớn hơn lực ma sát nghỉ cực đại:
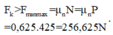
b) Muốn vật chuyển động thẳng đều, lực đẩy nằm ngang phải có độ lớn bằng độ lớn của lực ma sát trượt:
![]()