Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chỉ gần bằng. Có sự chênh lệch này là do sự thất thoát nhiệt do truyền cho môi trường xunh quanh.

1. Nhiệt độ của chì nay sau khi có sự cân bằng nhiệt là 40 độ C.
2. Nhiệt lượng nước thu vào là \(Q=C_{nước}.m_{nước}.\Delta t=4200.0,4.\left(40-30\right)=16800J.\)
3. Nhiệt lượng chì tỏa ra bằng nhiệt lượng nước thu vào tức là
\(Q_{tỏa}=Q_{thu}\)
=> \(C_{chì}.m_{chì}.\Delta t_2=16800\)
=> \(C_{chì}=\frac{16800}{1,25.80}=168\frac{J}{Kg.K}\)
1) nhiệt độ chì cân bằng là 40
2) nhiệt lượng nước là 16800
3) nhiệt dung riêng chì 168

refer
a) Nhiệt độ cuối cùng của chì cũng là nhiệt độ cuối cùng của nước, nghĩa là bằng 60°C
b) Nhiệt lượng nước thu vào:
Q = m1C1(t – t1) = 4 190.0,25(60 – 58,5)
= 1 571,25J
c) Nhiệt lượng trên do chì tỏa ra, do đó tính nhiệt dung riêng của chì:
C2=Q/m2(t2–t)=1571,25/0,3(100–60)≈130,93J/kg.K

a) Nhiệt độ của chì ngay khi có cân bằng nhiệt là \(60^0C.\)
b) nhiệt lượng nước thu vào là:
\(Q_2=m_2.c_2.\left(t-t_2\right)=0,2.4200.\left(600-58,5\right)=1260J\)
c) nhiệt dung riêng của chì là:
Áp dụng phương trình cần bằng nhiệt, ta có:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\left(t_1-t\right)=m_2.c_2.\left(t-t_2\right)\\ \Leftrightarrow0,3.c_1.\left(100-60\right)=0,2.4200.\left(60-58,5\right)\\ \Leftrightarrow12c_1\Leftrightarrow1260\\ \Leftrightarrow c_1=105J/kg.K\)
d) Vì nhiệt dung riêng của vật phụ thuộc vào nhiều yếu tố nên có thể cao hoặc thấp nên kết quả tính được chỉ gần đúng giá trị ghi ở bảng nhiệt dung riêng.

a) Nhiệt độ của chì ngay khi có cân bằng là \(60^0C\)
b) Nhiệt lượng nước thu vào:
\(Q_2=m_2.c_2.\left(t-t_2\right)=0,25.4200.\left(60-58,5\right)=1575J\)
c) Nhiệt dung riêng của chì:
Thep phương tình cân bằng nhiệt:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\left(t_1-t\right)=m_2.c_2.\left(t-t_2\right)\\ \Leftrightarrow0,3.c_1.\left(100-60\right)=0,25.4200.\left(60-58,5\right)\\ \Leftrightarrow12c_1=1575\\ \Leftrightarrow c_1=131,25J/kg.K\)

a) Nhiệt lượng thu vào của nước: Q = mcΔt = 4200.0,25.1,5 = 1575 J
b) Tính nhiệt dung riêng của chì:
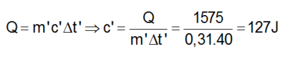
c) So với giá trị ghi ở bảng nhiệt dung riêng thì giá trị này bé hơn là do trong thí nghiệm, một lượng nhỏ nhiệt đã mất mát.

Ta nói làm cho nước nóng lên 60 độ tức tcb là 60o
Nhiệt lượng nước thu vào
\(Q_{thu}=0,25.4200\left(60-58,5\right)=1575J\)
Ta có phương trình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\\ \Leftrightarrow0,3.c\left(100-60\right)=1575\\ \Leftrightarrow c=131,25\)
Do dự hao phí nên nhiệt dung riêng của đồng có sự thay đổi từ môi trường ngoài

Tóm tắt:
\(m_1=300g=0,3kg\)
\(t_1=100^oC\)
\(m_2=250g=0,25kg\)
\(t_2=58,5^oC\)
\(t=60^oC\)
\(c_2=4200J/kg.K\)
=========
a) \(t=?^oC\)
b) \(Q_2=?J\)
c) \(c_1=?J/kg.K\)
So sánh với nhiệt dung riêng của chì trong bảng:
Giải:
a) Nhiệt độ của chì ngay khi có cân bằng là \(t=60^oC\)
b) Nhiệt lượng nước thu vào:
\(Q_2=m_2.c_2.\left(t+t_2\right)\)
\(\Leftrightarrow Q=0,25.4200.\left(60-58,5\right)=1575J\)
c) Nhiệt dung riêng của chì:
Thep phương tình cân bằng nhiệt:
\(Q_1=Q_2\)
\(\Leftrightarrow m_1.c_1.\left(t_1-t\right)=1575\)
\(\Leftrightarrow c_1=\dfrac{1575}{m_1.\left(t_1-t\right)}\)
\(\Leftrightarrow c_1=\dfrac{1575}{0,3.\left(100-60\right)}\)
\(\Leftrightarrow c_1=131,25J/kg.K\)
Nhiệt dung riêng này lớn hơn so với nhiệt dung riêng của chì trong bảng

Tham khảo nha em:
a) Nhiệt độ cuối cùng của chì cũng là nhiệt độ cuối cùng của nước, nghĩa là bằng 60°C
b) Nhiệt lượng nước thu vào:
Q = m1C1(t – t1) = 4 190.0,25(60 – 58,5)
= 1 571,25J
c) Nhiệt lượng trên do chì tỏa ra, do đó tính nhiệt dung riêng của chì:
\(C_2=\dfrac{Q}{m_2\left(t_2-t\right)}=\dfrac{1571,25}{0,3\left(100-60\right)}\approx130,97J\)/kg.K
d) Nhiệt dung riêng của chì tính được với nhiệt dung riêng của chì tra trong bảng gần bằng nhau, vì đã bỏ qua nhiệt lượng truyền cho môi trường xung quanh.

Ta nói nước nóng lên 60o thì \(t_{cb}=60^o\)
Nhiệt lượng nước thu vào
\(Q_{thu}=0,15.4200\left(60-58,5\right)=945J\)
Ta có phương trình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\\ 0,2.c_1\left(100-60\right)=945\\ \Rightarrow c_1=118,125J/Kg.K\)
Do có sự hao phí từ môi trường ngoài