Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

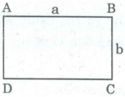
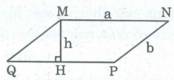
* Xét hình chữ nhật ABCD có chiều dài AB = a, chiều rộng AD = b.
Ta có: S A B C D = ab.
* Hình bình hành MNPQ có góc M là góc tù, MN = a, cạnh MQ = b
Kẻ đường cao MH. Ta có: S M N P Q = MH.a
Theo bài ra, ta có: MH.a = 1/2 ab
Suy ra: MH = 1/2 b hay MH = MQ/2
Tam giác MHQ vuông tại H và MH = MQ/2
Cạnh đối diện góc nhọn bằng một nửa cạnh huyền nên ∠ (MQH) = 30 0
Vậy góc nhọn của hình bình hành bằng 30 0 .

a b b a h A B H
Diện tích hình chữ nhật là \(ab\).
Diện tích hình bình hành là \(a.h\) với \(h=AH\) là đường cao.
Trong tam giác vuông HAB có AB là cạnh huyền, ta có \(AH< AB\), hay là \(h< a\)
Vậy \(ah< ab\). Suy ra diện tích hình chữ nhật lớn hơn.

Hình chữ nhật có hai cạnh là a và b nên S c h ữ n h ậ t = ab
Hình bình hành có hai cạnh là a và b. Kẻ đường cao ứng với cạnh bằng ạ thì h < b (vì cạnh góc vuông nhỏ hơn cạnh huyền).
Nếu kẻ đường cao ứng với cạnh bằng b thì h < a (cạnh góc vuông nhỏ hơn cạnh huyền).
Diện tích của hình bình hành là: S h ì n h b ì n h h à n h = a.h = b.h'
Mà h < b và h' < a nên S h ì n h b ì n h h à n h < S c h ữ n h ậ t

Diện tích hình chữ nhật: `S = b . (a+1+a) = b(2a+1) = 2 . 2,6 = 5,2 m^2`