Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B

Chọn A
+ Thế năng của vật tại vị trí lò xo giãn cực đại:
![]()
Động năng khi đó: Wđ = 0.
Ngay sau khi tiến hành giữ chặt lò xo tại vị trí cách vật một đoạn l, lò xo còn lại dao động có chiều dài tự nhiên là: l’0
Coi lò xo giãn đều, nên ta có:
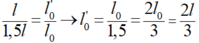
→ Độ cứng của lò xo mới là: k’ = 1,5k
+ Thế năng của vật ngay sau khi giữ:
![]()
Động năng của vật ngay sau khi giữ: W’đ = 0
Cơ năng của vật ngay sau khi giữ:
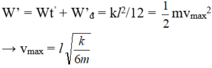

Chọn B
+ Vận tốc của hai vật sau va chạm: (M + m)V = mv
![]()
+ Tọa độ ban đầu của hệ hai vật:
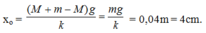
![]()



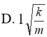

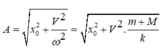
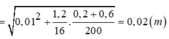

Với biên độ thỏa mãn để vật 2 luôn nằm trên vật 1 thì