Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện : 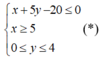
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.
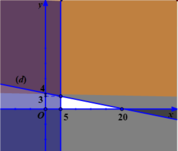
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tam giác) không tô màu trên hình vẽ
Giá trị lớn nhất của M( x; y) =x+ 6y đạt tại một trong các điểm (5;3) ; ( 5;0) và ( 20; 0).
Ta có M (5; 3) = 23; M( 5; 0) = 5 và M( 20; 0) = 20.
+ Suy ra giá trị lớn nhất của M( x; y) bằng 23 tại ( 5; 3) tức là nếu đặt thời lượng quảng cáo trên sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.

Tham khảo:
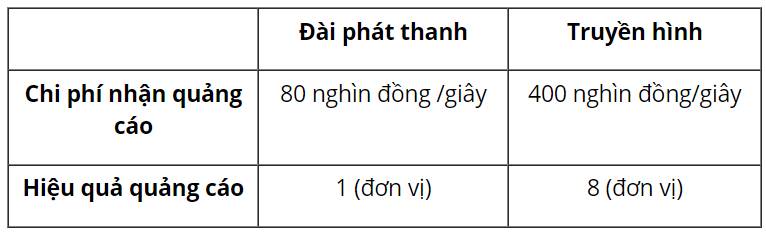
Gọi x và y là số giây quảng cáo trên đài phát thanh và trên truyền hình.
Khi đó \(x \ge 0;y \ge 0\)
160 triệu đồng=160000 (nghìn đồng)
Chi phí quảng cáo x giây trên đài phát thanh và y giây trên truyền hình là \(80x + 400y\)(nghìn đồng)
Vì công ty dự chi tối đa 160 triệu đồng nên ta có
\(80x + 400y \le 160000\)\( \Leftrightarrow x + 5y \le 2000\)
Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây nên ta có: \(x \le 900\)
Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây nên ta có: \(y \le 360\)
Ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{l}}
{x \ge 0}\\
{y \ge 0}\\
{x + 5y \le 2000}\\
{x \le 900}\\
{y \le 360}
\end{array}} \right.\)
Xác định miền nghiệm là miền ngũ giác OABCD với:
A(900;0); B(900;220); C(200;360); D(0;360)
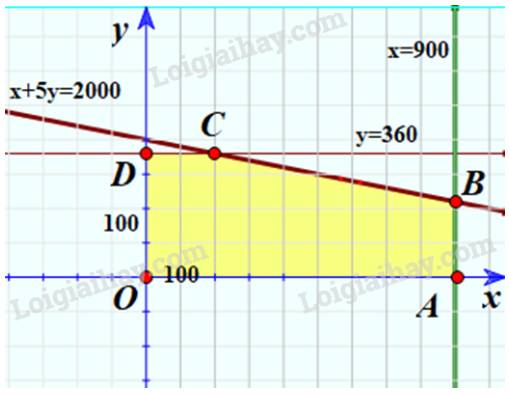
Hiệu quả quảng cáo là: \(F\left( {x;y} \right) = x + 8y\)
Ta có:
\(F\left( {0;0} \right) = 0\)
\(F\left( {900;0} \right) = 900 + 8.0 = 900\)
\(F\left( {900;220} \right) = 900 + 8.220 = 2660\)
\(F\left( {200;360} \right) = 3080\)
\(F\left( {0;360} \right) = 2880\)
Vậy công ty cần đặt thời gian quảng cáo trên đài phát thanh là 200 giây và trên truyền hình là 360 giây thì hiệu quả nhất.

Gọi x, y lần luợt là số lần phát quảng cáo vào khoảng 20h30 và vào khung giờ 16h00-17h00. \((x,y \in \mathbb{N})\)
Trong toán học, các điều kiện để đáp ứng nhu cầu trên của công ty đuợc thể hiện là:
+) ít nhất 10 lần quảng cáo vào khoảng 20h30: \(x \ge 10\)
+) không quá 50 lần quảng cáo vào khung giờ 16h00-17h00: \(y \le 50\)
+) chi không quá 900 triệu đồng: \(30.x + 6.y \le 900\)

- Gọi số xe loại A và loại B cần dùng là x và y xe .
=> Số tiền là : \(T=4x+3y\)
Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
Ta có :

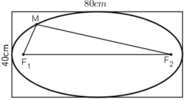
Giả sử Elip có phương trình 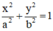
Độ dài trục lớn bằng 80cm ⇒ 2a = 80cm ⇒ a =40cm
Độ dài trục nhỏ bằng 40cm ⇒ 2b = 40cm ⇒ b = 20cm
Khi đó 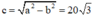 ⇒ F1F2 = 2c = 40√3 cm
⇒ F1F2 = 2c = 40√3 cm
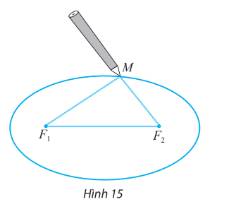
Khoảng cách từ vị trí hai chiếc đinh F1, F2 đến hai mép là:
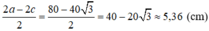
Độ dài vòng dây cuốn: MF1 + MF2 + F1F2 = 2a + 2c = 80 + 40√3 ≈ 149,3cm.

Từ giải thiết ta có: \(2a = 80 \Rightarrow a = 40,2b = 40 \Rightarrow b = 20\)
Suy ra, \(c = \sqrt {{a^2} - {b^2}} = 20\sqrt 3 \)
Suy ra vị trí đinh cách mép là \(a - c = 40 - 20\sqrt 3 = 5,36\) cm
Chiều dài vòng dây là \(2a + 2c = 2.40 + 2.20\sqrt 3 = 149,28\) cm
Vậy phải ghim hai cái đinh cách các mép tấm bìa 5,36 cm và lấy vòng dây có độ dài là 149,28 cm

Ta có: 2a = 80 => a = 40
2b = 40 => b = 20
c2 = a2 – b2 = 1200 => c = 20√3
Phải đóng đinh tại các điểm F1 , F2 và cách mép ván:
F2A = OA – OF2 = 40 – 20√3
=> F2A = 20(2 – √3) ≈ 5,4cm
Chu vi vòng dây bằng: F1.F2+ 2a = 40√3 + 80
=> F1.F2 + 2a = 40(2 + √3)
F1.F2 + 2a ≈ 149,3cm

+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện :
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.
Tại sao lại là M(x;y) = x + 6y ạ