Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).
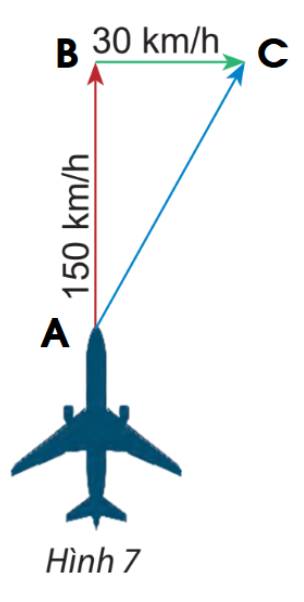
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Áp dụng định lý Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{150}^2} + {{30}^2}} = 30\sqrt {26} \)
Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h

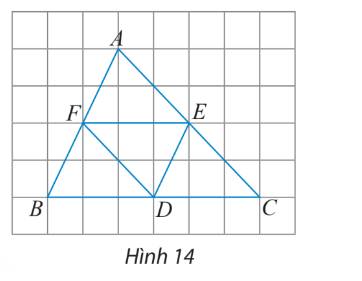
Từ giả thiết ta có:
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
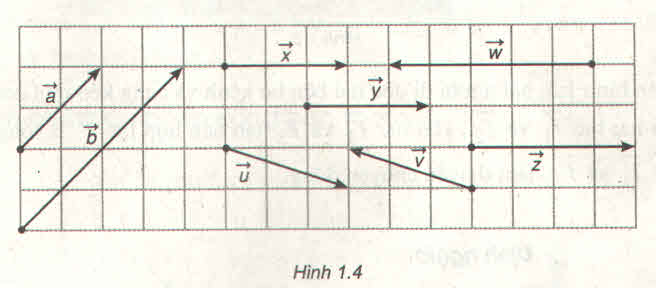
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

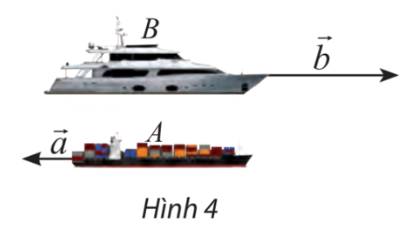
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)


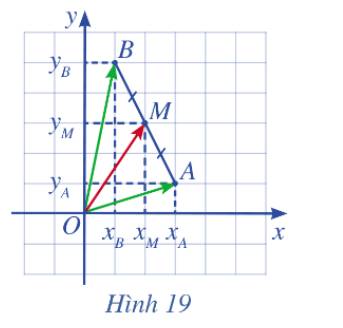
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

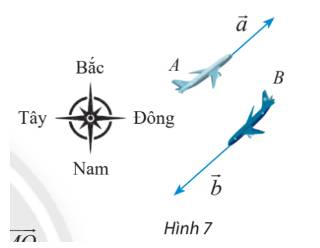
Vecto \(\overrightarrow a ,\;\overrightarrow b \) là vecto vận tốc của máy bay A và máy bay b.
Do đó \(\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|\) lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: \(\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800\)
\( \Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}\)
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó \(\overrightarrow b = - \frac{4}{3}\overrightarrow a \)

a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)

Tọa độ của vecto \(\overrightarrow {OM} \) là tọa độ của điểm M (trong đó O là gốc tọa độ)

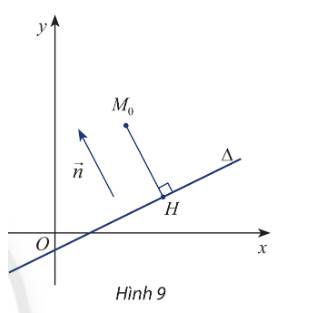
a) Ta có: \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Mà H là hình chiếu vuông góc của \({M_0}\) trên \(\Delta \) nên \(H{M_0} \bot \Delta \)
Mặt khác vectơ pháp tuyến \(\overrightarrow n \) cùng vuông góc với \(\Delta \)
Suy ra \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương (đpcm)
b) Ta có: \(\overrightarrow n = (a;b)\) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Suy ra \(p = \overrightarrow n .\overrightarrow {H{M_0}} = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)\) (1)
Mà H thuộc đường thẳng \(\Delta \) nên tọa độ điểm H thỏa mãn phương trình đường thẳng \(\Delta \)
Thay tọa độ điểm H vào phương trình \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) ta có:
\(a{x_H} + b{y_H} + c = 0 \Leftrightarrow c = - \left( {a{x_H} + b{y_H}} \right)\)
Thay \(c = - \left( {a{x_H} + b{y_H}} \right)\) vào (1) ta có
\(p = a{x_0} + b{y_0} + c\) (đpcm)
c) Ta có: \(p = \overrightarrow n .\overrightarrow {H{M_0}} \Leftrightarrow \overrightarrow {H{M_0}} = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)




Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).