Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
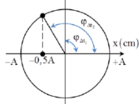
+ Từ vị trí cân bằng kéo vật xuống phía dưới để lò xo giãn 10cm rồi thả nhẹ => A = 10cm.
+ Lực phục hồi triệt tiêu tại vị trí cân bằng Δt1 = T/4
+ Lực đàn hồi triệt tiêu khi vật qua vị trí lò xo không giãn:
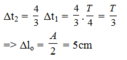
Vậy chu kì dao động của con lắc là: 

+ Trong quá trình dao động của con lắc lò xo treo thẳng đứng.
· Lực phục hồi triệt tiêu tại vị trí cân bằng.
· Lực đàn hồi bị triệt tiêu tại vị trí lò xo không biến dạng.
+ Từ hình vẽ ta có Δt1 = 0,25T và

Đáp án A

Đáp án C
Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 2.10 80 = 2 , 5 cm.
Kéo vật đến vị trí lò xo dãn 7,5 cm rồi thả nhẹ → vật sẽ dao động với biên độ A = 5 cm → E = 0 , 5 k A 2 = 0 , 1 J .
Lực đàn hồi của lò xo có độ lớn nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng, nếu chọn chiều dương hướng xuống vị trí này ứng với x = − 2 , 5 cm → E d = 1 2 k A 2 − x 2 = 1 2 80 0 , 05 2 − 0 , 025 2 = 0 , 075 J.
→ Thế năng của vật tại vị trí này là E t = E – E d = 0 , 1 – 0 , 075 = 0 , 025 J .
Lưu ý rằng thế năng của vật bằng tổng thế năng đàn hồi và thế năng trọng trường.
→ Thế năng đàn hồi của vật là E d h = 0 , 025 − 0 , 2.10.0 , 025 = − 0 , 025 J.

Đáp án D
Phương pháp: Sử dung̣ đường tròn lương̣ giác
Lực hồi phục có chiều luôn hướng về VTCB
Lực đàn hổi sinh ra khi lò xo bị biến dạng và có xu hướng đưa lò xo về trạng thái không biến dạng
Cách giải:
Tần số góc:
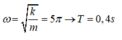
Độ dãn của lò xo ở VTCB: ∆ l = m g k = 4 cm
Kéo vật thẳng đứng xuống dưới để lò xo dãn 12cm rồi thả nhẹ cho vật dao động điều hoà => Biên độ dao động: A = 12 – 4 = 8cm
Biểu diễn trên đường tròn lượng giác khoảng thời gian hai lực cùng chiều (mô tả bởi phần trắng trên đường tròn)
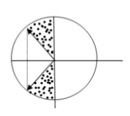
Từ đường tròn lượng giác => t = 5T/6 = 1/3 (s)


Lực kéo về triệt tiêu khi đi qua vị trí cân bằng.
Lực đàn hồi triệt tiêu khi đi qua vị trí lò xo k giãn
Tị trí cân bằng cách vị trí lò xo k giãn 1 đoạn là deltal0=mg/k (1)
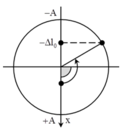
Từ đường tròn, chia khoảng đi từ biên dưới lên đên vị trí lò xo k giãn làm 4 tức là 1/4 chu kỳ phải bị chia làm 3 xem hình vẽ trên nhé. Khi đó thấy được vị trí lò xo k giãn có li độ -A/2 hay deltal0=A/2 thế vào (1) có được đáp án (để ý T bằng 2 pi căn mờ trên ka)
Giả sử trục tọa độ có gốc ở vị trí cân bằng, chiều dương hướng xuống
Lực đàn hồi triệt tiêu ở vị trí có li độ \(x=-\Delta l_0=-\dfrac{mg}{k}\)
Lực hồi phục triệt tiêu ở gốc tọa độ \(x=0\)
Biểu diễn bằng véc tơ quay, thì để lực hồi phục triệt tiêu véc tơ quay góc \(\alpha = 90^0\)
Suy ra lực hồi phục triệt tiêu thì véc tơ quay một góc là: \(90^0.\dfrac{4}{3}=120^0\)
\(\Rightarrow\dfrac{\Delta l_0}{A}=1/2\)
\(\Rightarrow\dfrac{mg}{kA}=1/2\)
\(\Rightarrow k/m\)
\(\Rightarrow T\)

Đáp án C
Để đơn giản, ta có thể chia quá trình chuyển động của vật thành hai gia đoạn.
Giai đoạn chuyển động từ biên dưới đến vị trí lò xo khống biến dạng → lực đàn hồi là hợp lực của lò xo và dây tương ứng với lò xo có độ cứng k = k 1 + k 2 = 40 N / m .
Giai đoạn hai từ vị trí lò xo không biến dạng đến vị trí lò xo bị nén cực đại, lúc này dây bị chùng nên không tác dụng lực đàn hồi lên vật.
+ Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 40 = 2 , 5 cm = 0,5A.
→ Thời gian chuyển động từ biên dưới đến vị trí lò xo không biến dạng là t 1 = T 1 3 = 2 π 3 m k = 2 π 3 0 , 1 40 = π 30 s
→ Vận tốc của vật ngay thời điểm đó v 0 = 3 2 ω A = 3 2 40 0 , 1 .5 = 50 3 cm/s
+ Khi không còn lực đàn hồi của dây, ta xem vật dao động điều hòa quanh vị trí cân bằng mới, nằm dưới vị trí cân bằng cũ một đoạn = 0 , 1.10 10 − 2 , 5 = 7 , 5 c m
→ Biên độ dao động mới A ' = 2 , 5 + 7 , 5 2 + 50 3 10 2 = 5 7 ≈ 13 , 23 cm.
+ Thời gian để vật đến biên trên tương ứng là t 2 = T 2 360 0 a r cos 10 5 7 = 0 , 2 π 360 0 a r cos 10 5 7 ≈ 0 , 071 s.
→ Tổng thời gian t = t 1 + t 2 = 0 , 176 s .

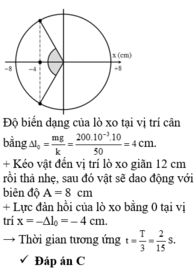

Bạn tham khảo bài tương tự như thế này nhé.
Câu hỏi của Đào Hiếu - Vật lý lớp 12 | Học trực tuyến