Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khối lượng M của phần nước đá tan thành nước sau khi thả thỏi sắt nóng có nhiệt độ t ° C vào cốc nước đá ở 0 ° C được xác định bởi điều kiện cân bằng nhiệt:
M λ = cmt ⇒ M = cmt/ λ
trong đó λ là nhiệt nóng chảy riêng của nước đá, c là nhiệt dung riêng của thỏi sắt có khối lượng m.
Thay số, ta tìm được :
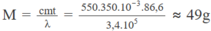

1.
Từ biểu thức tính khối lượng riêng \(\rho = \frac{m}{V}\), ta thấy khối lượng riêng tỉ lệ nghịch với thể tích, mà thể tích của vật lại phụ thuộc vào nhiệt độ nên khối lượng riêng phụ thuộc vào nhiệt độ.
2.
Thể tích của hợp kim là:
\(\rho = \frac{m}{V} \Rightarrow V = \frac{m}{\rho } = \frac{{100}}{{10,3}} = \frac{{1000}}{{103}}(c{m^3})\)
Gọi khối lượng và thể tích của đồng lần lượt là m1, V1, của bạc là m2, V2
Ta có:
\({V_1} + {V_2} = V \Leftrightarrow \frac{{{m_1}}}{{{\rho _d}}} + \frac{{{m_2}}}{{{\rho _b}}} = V \Leftrightarrow \frac{{{m_1}}}{{8,9}} + \frac{{{m_2}}}{{10,4}} = \frac{{1000}}{{103}}\) (1)
Mặt khác, ta có khối lượng của hợp kim là 100 g
\( \Rightarrow {m_1} + {m_2} = 100\) (2)
Từ (1) và (2) => m1 = 5,76 g; m2 = 94,24 g
Chú ý: Đơn vị của \(\rho \)là g/cm3 thì đơn vị của khối lượng m là g và của thể tích V là cm3

Nhiệt lượng thu vào của đồng thau và nước là
\( Q_{thu}=c_{Cu}m_{Cu}(t-8,4) +c_{nc}.m_{nc}.(t-8,4).(1) \)
Nhiệt lượng tỏa ra của miếng kim loại là
\( Q_{toa}=c_{kl}m_{kl}(100-t) .(2) \)
Khi hệ cân bằng nhiệt thì \(Q_{thu} = Q_{toa}\)
Thay số với nhiệt độ lúc cân bằng t = 21,5 độ C. Ta sẽ tính được nhiệt dung riêng của kim loại là
\(c_{kl} = \frac{0,128.0,128.10^3.13,1+0,21.4,18.10^3.13,1}{0,192.79} = 0,772.10^3\)(J/kg.K)

Bỏ qua sự truyền nhiệt ra môi trường bên ngoài. Nhiệt dung riêng của đồng thau là
0,128.103 J(kg.K).
Hướng dẫn giải.
Nhiệt lượng mà nhiệt lượng kế và nước thu vào :
Qthu = Q1 + Q2 = (m1c1 + m2c2)(t – t1).
Nhiệt lượng mà miếng kim loại tỏa ra :
Qtỏa = Q3 = m3c3. ∆t3 = m3c3 (t3 – t).
Trạng thái cân bằng nhiệt :
Q1 + Q2 = Q3.
⇔ (m1c1 + m2c2)(t – t1) = m3c3. ∆t3 = m3c3 (t3 – t).
\(\Rightarrow c_3=\dfrac{m_1c_1+m_2c_2\left(t-t_1\right)}{m_3\left(t_3-t\right)}\)
\(\Rightarrow c_3=\dfrac{\left(0,128.0,128+0,21.4,18\right).\left(21,5-8,4\right)10^3}{0,192.\left(100.21,5\right)}\)
=> c3 = 0,78.103 J/kg.K

Nhiệt lượng mà nhiệt lượng kế và nước thu vào :
Qthu = Q1 + Q2 = (m1c1 + m2c2)(t – t1).
Nhiệt lượng mà miếng kim loại tỏa ra :
Qtỏa = Q3 = m3c3. ∆t3 = m3c3 (t3 – t).
Trạng thái cân bằng nhiệt : Q1 + Q2 = Q3.
⇔ (m1c1 + m2c2)(t – t1) = m3c3. ∆t3 = m3c3 (t3 – t).
=>
=>
=> c3 = 0,78.103 J/kg.K

Nhiệt lượng bình nhôm và nước thu vào là
\(Q_{thu} = Q_{Al}+Q_{nc} = c_{Al}m_{Al}(t-20)+c_{nc}m_{nc}(t-20) \) (1)
Nhiệt lượng miếng sắt tỏa ra khi thả vào bình nhôm chứa nước là
\(Q_{toa} = Q_{Fe} = c_{Fe}m_{Fe}(75-t) .(2)\)
Bỏ qua sự truyền nhiệt nên ta có khi có sự cân bằng nhiệt thì nhiệt lượng tỏa ra đúng bằng nhiệt lượng thu vào
\(Q_{thu} = Q_{toa}\)
=> \( c_{Al}m_{Al}(t-20)+c_{nc}m_{nc}(t-20) = c_{Fe}m_{Fe}(75-t) \)
Thay số thu được t = 24,890C.

Hướng dẫn giải.
Nhiệt lượng mà nhôm và bình nước thu vào :
Qthu = Q1 + Q2 = (m1c1 + m2c2)(t – t1).
Nhiệt lượng do sắt tỏa ra là :
Qtỏa = Q3 = m3c3. ∆t3 = m3c3 (t3 – t).
Trạng thái cân bằng nhiệt :
Q1 + Q2 = Q3.
⇔ (m1c1 + m2c2)(t – t1) = m3c3. ∆t3 = m3c3 (t3 – t)
\(\Rightarrow t=\dfrac{\left(m_1c_1+m_2c_2\right)\left(t-t_1\right)}{m_1c_1+m_2c_2+m_3c_3}\)
\(\Rightarrow t=\dfrac{\left(0,5.0,92+0,118.4,18\right)10^3.20+0,2.0,46.10^3.75}{\left(0,5.0,92+0,118.4,18+0,2.0,46\right).10^3}\)
=> t ≈ 25oC.
bạn à,cái hướng dẫn giải này bn chép trên mạng hả, trên đó nó thay số sai ,c\(_1\) phải là 0,896.10\(^3\) chứ không phải 0,92.10\(^3\)

Ta có m 1=0,5kg
m2=0,118kg
t1 +12 =20độC
m3=0,2kg
t3=75độ
c1=4180J/kgK
C2=920
C3=460
Bình nhôm và nước là 2 đai lượng thu nhiệt còn sắt tỏa nhiêt, nên ta có :
Q NHÔM =mc\(\Delta t\)
=0,5 x 920 (t-20)
Qnươc =mc\(\Delta t\) =0,118 x 4180 (t - 20)
Q sắt = mc \(\Delta t\) =0,2 x 460 (75 - t)
Theo pt cân băng nhiêt ta có:Q1+Q2 =Q3
Thay vào 0,118x4180(t-20) + 0,5x920(t-20) ==0,2 x 460(75-t)
Giải tiếp pt trên rồi tìm t nhé